|
I decided that a resource post was long overdue for the #summerblogchallenge, so I thought I'd post one of my favourite lessons. I put this together after discovering the fantastic Gapminder website a couple of years ago, and it's designed to provide a nice real-life link for exponential growth.
In the spirit of encouraging personal positive thinking, I've decided to start a new Sunday blog series on the best lesson I've taught the previous week.
This week my pick actually covers two lessons of work, and was delivered to my Year 9s on Thursday and Friday. To provide a bit of context, we're trialling the Mastery Pathway with KS3 this year, and pupils sat the Elementary 4 test on Tuesday, covering negative numbers, substitution and lots of fractions and decimals work. They passed the previous three tests pretty well, but this one caused some difficulties, with marks ranging from 30% to 70%. After doing a bit of analysis on the results, I decided that my first topic for re-teaching would be working with fractions and decimals, particularly ordering and converting between the two representations. Teaching trigonometry (1)16/4/2015 I've been teaching trigonometry from scratch with Year 10 this week, so thought it would be a good opportunity to blog about the way I introduce sine, cosine and tangent. This is another sequence of lessons I love teaching, because it's one of my tried and tested approaches and seems to work well each year.
We started the lesson with a few quick questions on Pythagoras' theorem (I used these ones). I taught them Pythagoras' theorem way back in November, but most of them remembered how to solve the problems with a bit of prompting. I was aiming to refresh identification and use of the word "hypotenuse" and also provide a link from something they'd previously learned about right-angled triangles. After we'd done this, it was on to the first bit of the trigonometry introduction! Having taught this to nearly all of my KS3 groups at some point in the last few months, I think I'm becoming something of an expert. This year, we've started the Mastery Pathway at KS3, and nearly all of our students in Years 7, 8 and 9 (unsurprisingly) had gaps in their understanding of fractions. So I've now taught this about five or six times; it's true what they say about practice making perfect (or pretty close). Two major changes this year have been use of the bar model (read about my discovery here) and linking cubes. I'm trying to do a lot more in concrete situations before moving to rules, and using manipulatives and models seems to get the ideas to stick. 1. Start with a chocolate bar Think Cadbury's Dairy Milk (single bar), Kinder Bueno, Hershey Bars - anything which comes in a single row of squares or pieces of chocolate. The first thing I did was show the students some pictures of these chocolate bars, and get them to tell me each piece size as a fraction - e.g. the Bueno has four pieces, so if I eat one piece, I've eaten 1/4, two pieces is 2/4 and so on. We spent some time discussing what the numerator and denominator tell us about the different chocolate bars, and emphasising that the denominator told us about the size of one whole bar. 2. Move to a physical model I then gave students different amounts of link cubes, explaining that they were pretending these were squares of chocolate. I asked them to make me as many whole chocolate bars as they could - we used the Bueno 4 square model to start with. There were a few comments about how I'd not given them enough cubes in some cases (they were expecting multiples of four); I kept quiet and just told them to build what they could. Once they'd built for a bit, a couple of the students realised that this was the point of the task. We then collected ideas on the board and looked at different students' examples. I deliberately started using a bar model at this point to represent the cube pictures they were explaining. This is also a good point to get students to draw their models on the board themselves and explain what they've done. 3. Introduce improper fraction notation I took one example and modeled the use of fraction notation, drawing on our original chocolate examples. So 13/4 means 13 pieces of chocolate, and one whole bar has 4 pieces. We then discussed how this related to mixed number form:
4. Practise problems using cubes and diagrams I then gave students some problems to try for themselves. They started with more examples using four-square chocolate bars, then progressed to other sizes. I kept denominators fairly small to start with (2, 3, 4 and 5), just because modelling and drawing gets a little impractical with larger denominators. I encouraged students to use the cubes where necessary, and insisted they drew diagrams for the first few they attempted. Some students quickly spotted the "rule" and then began working without diagrams. Towards the end of the activity, we discussed what they had discovered as a shortcut method and why it worked. However, I haven't been pushing rules too much this year - I'd rather students thought about what they were doing, and if necessary got the right answer through drawing a diagram, rather than learn a rule which is quickly forgotten. 5. Work the opposite way Some of the classes I've tried this with were ready to move on to converting back the other way, either with diagrams or by applying understanding gained from working from improper to mixed within the same lesson. Some of them needed a little more consolidation work one way before we moved on. One lesson I'm learning this year is how important it is not to push too quickly; a new idea takes time to cement thoroughly, and I think it's worth working on one thing properly at a time, rather than charging ahead and progressively losing students along the way. If you're looking for questions quickly, Math Aids has a great worksheet generator, differentiable by easy, medium and hard denominators. |
Categories
All
Archives
August 2020
|
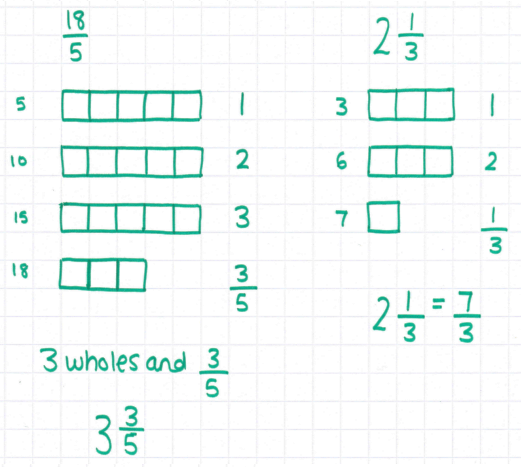
 RSS Feed
RSS Feed
