I decided that a resource post was long overdue for the #summerblogchallenge, so I thought I'd post one of my favourite lessons. I put this together after discovering the fantastic Gapminder website a couple of years ago, and it's designed to provide a nice real-life link for exponential growth.
This lesson looks at two different scenarios. It starts with the famous “Chessboard Problem” involving grains of rice on a chessboard. Pupils calculate how many grains of rice on the first few squares. This links to ideas about population growth; pupils plot a graph of population growth over the last 200 years and use their graph to predict what will happen in the year 2050. Finally, discuss limitations of the exponential model and real-life interpretations of why the model may not be accurate (e.g. lack of natural resources). I have used this successfully with a middle-ability group in Year 9, so prior knowledge of exponential graphs is not necessary.
|
Pupils start off by estimating the Earth’s population in 2050 and writing their answers on a Post-It - there will be some very interesting answers at this point!
We then go through the story of the Chessboard Problem, either as a discussion or by asking pupils to read through it themselves and then summarise as a class - a good literacy opportunity. Pupils work out how many grains of rice will be on the 32nd square of the chessboard, either independently or in groups. Encourage pupils to work systematically and show how they have got their answer. Pupils then plot this information on a graph- sometimes they need support in terms of a sensible scale for their axes. This results in the graph y = 2 to the power x. It's not necessary for pupils to use this algebraic representation during the lesson, but might be worth pointing out. |
|
|
After revealing the answer and providing a bit of context (the total amount of rice on all 64 squares would weigh over 100,000kg and be larger than Mount Everest), pupils then have a go at plotting a similar graph using world population data and comparing their initial estimate to the graph's predicition. Many of them will have instinctively used a linear model in their initial prediction.
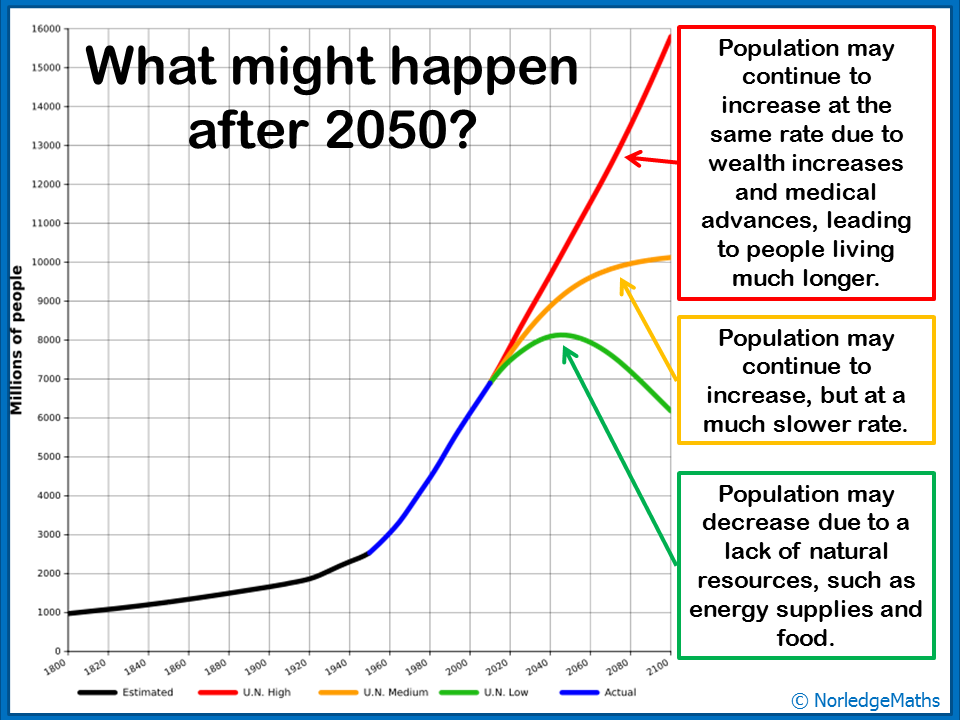
It's nice to have a discussion about why they think population is growing at such a rapid rate (better medicines, quality of life, scientific knowledge). Is it realistic for the population to continue growing at such a rate and consider what factors may limit population growth (lack of natural resources, physical space on the planet)? The video "What Stops Population Growth" from Gapminder is great to finish off the lesson - it's ten minutes long, but most of the pertinent points are within the first few minutes. |
|
|
Previous Posts |
RSS Feed
