Stuck in traffic on the way home today, and bored of listening to Katy Perry's latest offering on pretty much repeat on most of the local radio stations, I made a very exciting discovery on Radio 4. I caught the last fifteen minutes of the program Digital Human, which explores how the world around us has evolved in the Digital Age. The programme I caught the end of was on memory, and looked at the idea that our memory is getting worse because we now have information permanently at our fingertips through smartphones and the Internet. It's well worth a listen, but a couple of things on there gave me a lot of food for thought.
Transactional Memory
Now, I knew absolutely nothing about this until listening to this programme. Transactional memory refers to the fact that we know people (or increasingly, things) who have specialist knowledge about certain topics, and therefore we don't need to memorise the knowledge ourselves.
A couple of examples mentioned were a husband who knew everything about sport (and therefore his wife could just ask
him anything she wanted to know at any point, without needing to memorise as the information was readily available), and a dad who knew all the addresses, birthdays and anniversaries for his family - rather relevant to me, as every year around Christmas time, I inevitably call my mother for a list of addresses to send cards to.
The programme made the point that we have just swapped these specialist people for "things", such as our smartphones or computers, and rather than memorising the information, we are instead using our memory to remember where to find the information when needed.
This rang very true with me (and not just because of the Christmas card thing). I thought of all the times in the past I used to phone my dad when my computer blew up or something malfunctioned, but now my first port of call is Google (usually on another device if I've majorly virused something). If I've forgotten a minor point from S1 to teach my A Level class, I turn to the Internet first, rather than ask one of my comparatively many friends who work with statistics on a daily basis.
Jack, the fifteen year old, and his breakthrough Science Fair project
To finish off the programme, an interview was conducted with a fifteen-year-old living in Maryland, who had designed a rather complex early warning system for various types of cancer. Judging by his vocabulary and verbosity, the lad was obviously quite bright - however, I was amazed when he explained the complexity of his ideas (and confess to not understanding them fully!). He explained that he had taken some personal research he had done on the Internet, connected it with his school Biology work, done a bit of additional reading, then invented this fascinating bit of equipment that's cheaper and more effective than the current warning systems.
He discussed the fact that, without the Internet, his discovery would not have been possible, because he wouldn't have
had so many scientific journals and research documents readily available at his fingertips. Crucially, the interviewer said something right at the end of Jack's slot that really stuck with me: being smart used to be about knowing lots of facts, because information wasn't so easily accessible, but that being smart now means being able to access, filter and synthesise the vast amounts of information available to us. Which got me thinking on the third point...
How does our education system relate to this?
This is something I've thought about a lot before, and I've read quotes from mathematicians saying stuff along the same lines: if your job involves mathematics on a professional level, you don't try to memorise loads of formulae, as you can just look them up as and when you need to. Another point the programme made was on the function of memory - it is designed that we should forget things after they have stopped being useful. One researcher talked about the brain being a "behaviour machine", not a "memory machine", which adapts to the situations we find ourselves in as we go through life and alters memory accordingly.
Which all boils down to one thing, really. Why, with all this technology at our fingertips, and continually evolving ways to access information as and when we need it, do we still have an exam system in Mathematics that focuses so strongly on memorising facts (which inevitably disappear from the heads of Year 11s very soon after they finish their exams), and not techniques for finding, synthesising and finding applications for existing information, which is surely a much more important skill to have to survive in the Digital Age?
The programme is still available via the BBC using the link above. Gotta love blasts from the past!

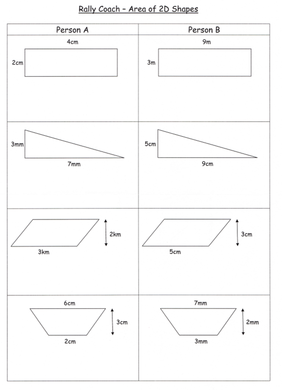
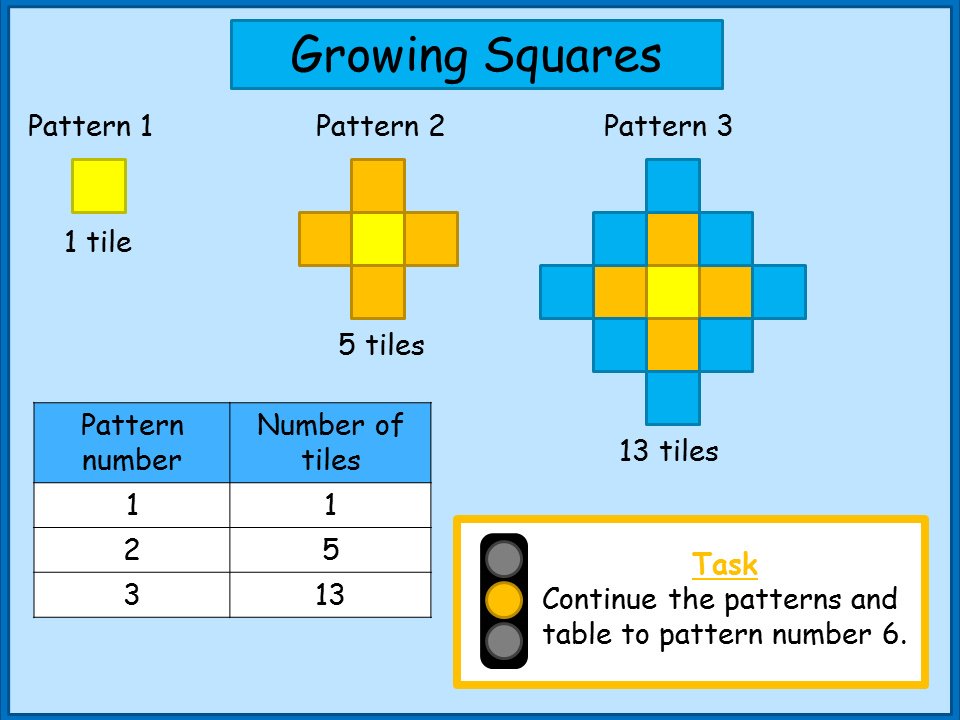

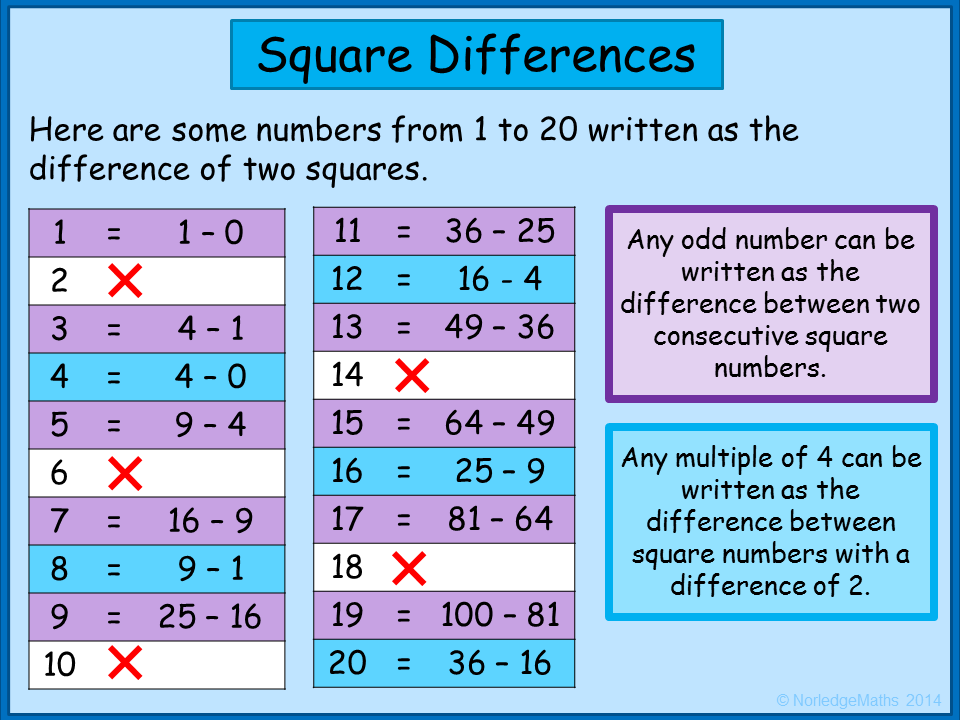

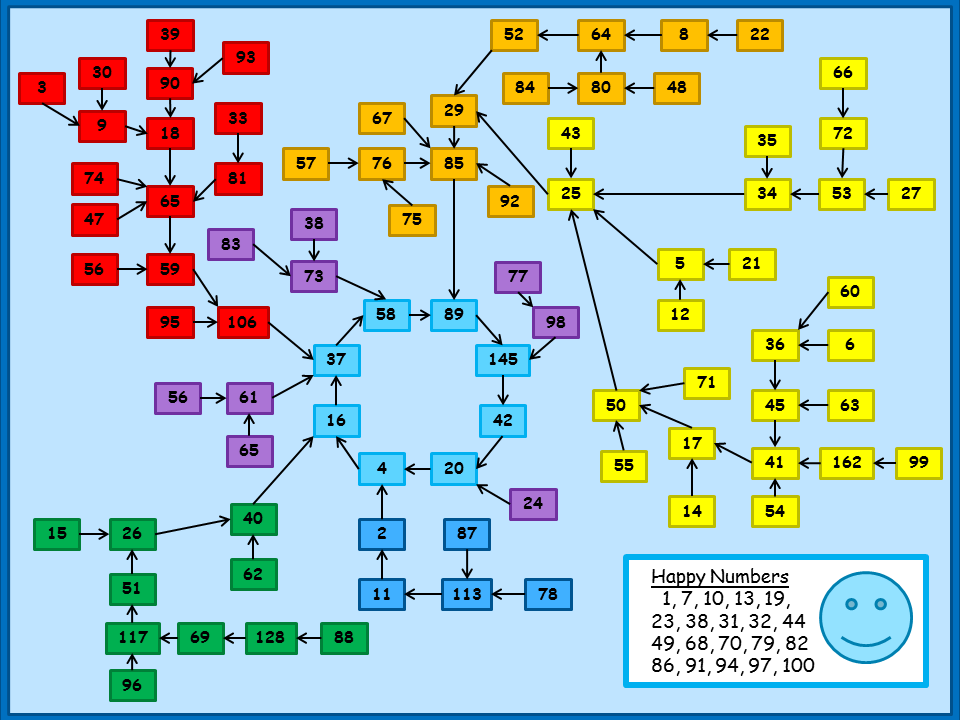
 RSS Feed
RSS Feed
