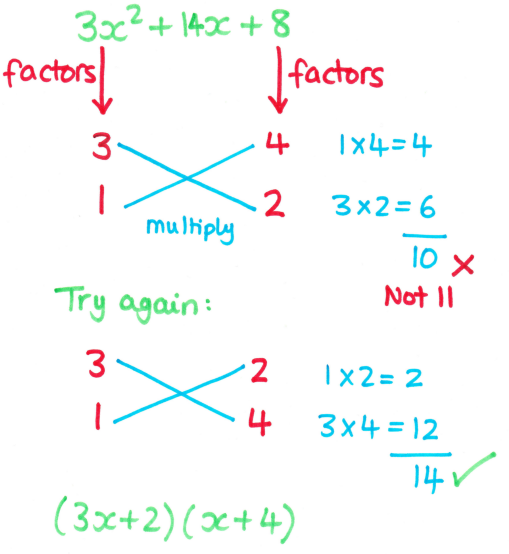
Anyway, last week I went on a training course for the new 9-1 GCSE from Edexcel. All interesting stuff about the exam changes, but my biggest takeaway was this: the "Cross Method" for factorising quadratics with a > 1. I was keen to give it a go with Year 10, so after doing some simple quadratics with a = 1 (mostly OK, apart from the usual wrangles with negative numbers and having to unteach negative add negative is positive), we tried a few with a > 1.
I started with my usual "reverse grid method and reason it out" approach; blank stares and confusion. I then showed them the same question using the "Cross Method". Cue shouts of "oh that's easy!" and "why did you even show us that first way?!".
- It's an easy way into the problem; it turns a complicated quadratic into a little number puzzle.
- It helps students to structure and record their trials. It's useful for both them and me to be able to see what numbers they have tried.
- It works for all quadratics. I probably wouldn't encourage this for simple quadratics with a = 1, but it would work!
- It really does help with issues with negative numbers, as students have to do the calculation at the side, which makes them think more carefully about their working.
I think I'll be using this a lot more in future! It's not a substitute for understanding, but once the understanding is in place, it provides structure and organisation for the trial and error method.
 RSS Feed
RSS Feed
