#MathsConf13 took place last Saturday, and as usual, was another fantastic day of cheap CPD. Sadly, I missed the London conference in the summer, so I was really looking forward to this one. It definitely didn't disappoint, despite being a bit of a struggle at nearly 8 months pregnant!

One highlight of the day was the keynote from Matt Parker; I have to confess to spending the first few minutes wondering why this bloke looked so familiar until I realised that I'd seen him in the superb Numberphile videos.  He was highly entertaining, but also gave a few decent ideas for use in the classroom, such as thinking about images as RGB spreadsheets and creating a mega-Menger sponge or a fractal Christmas tree.

My three speed-dates were as follows:

• Catching up with a colleague from my old school - I know, this isn't really what speed dating is for, but we did have a good chat about their decisions regarding GCSEs and A Levels!
• Paul (@PaulRodrigo2718 ), who showed me his method for scaffolding problem-solving questions at GCSE.
• Richard (@TickTockMaths), who shared the absolutely superb dudamath.com, which I'd not seen before but has so much going on that its potential for use in the classroom seems massive.

Rather than attempting to blog about each workshop (I still haven't finished my #mathsconf7 round-up - now unlikely to ever happen!), I decided to make the most of my time off by doing a bit of relaxing colouring-in - so this conference's workshop posts are in "visual blog" format. I attended:

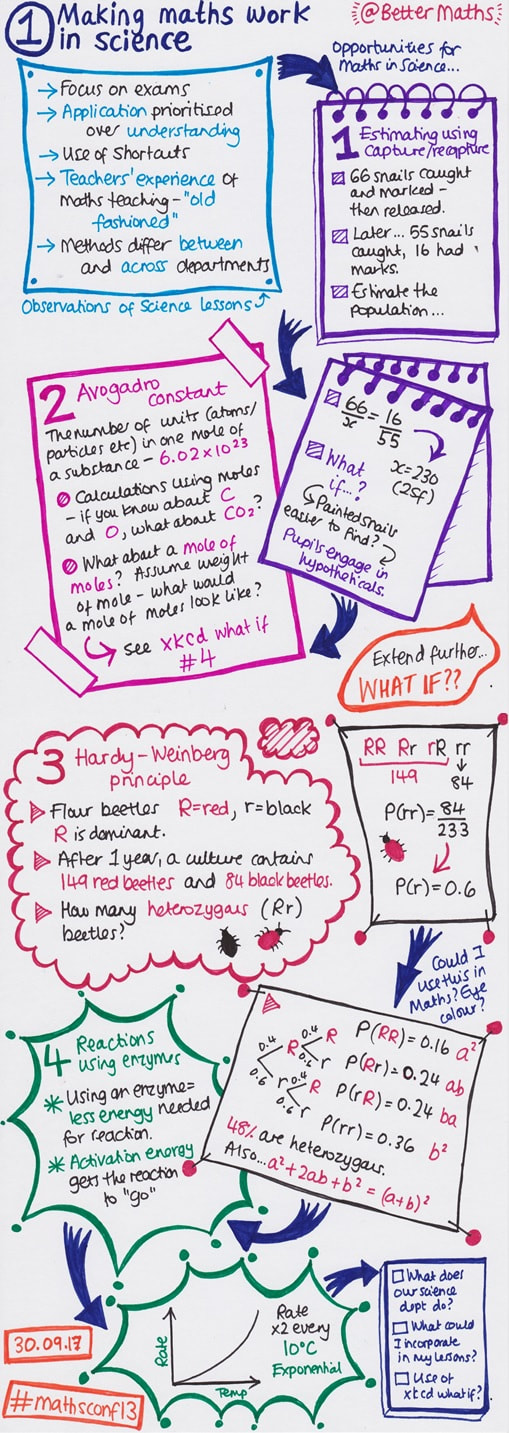
1. Making Maths Work in Science with Luke Graham (@BetterMaths);
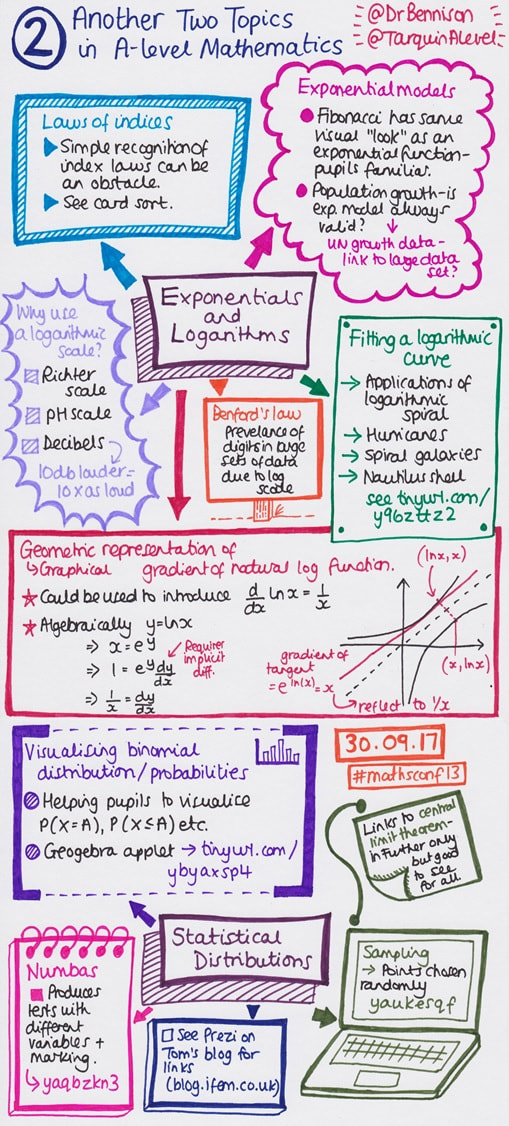
2. Another Two Topics in A Level Mathematics with Tom Bennison (@DrBennison) and Ed Hall (@TarquinAlevel);
3. Things to Do With your Large Data Set with Stella Dudzic;
4. Problem Solving - Getting to Grips with the Overarching Theme 2 in the New Maths A-level with Dan Rogan.

The Prezi from the session and links to all of the applets and resources mentioned can be found on Tom's blog post.

Session 2 at #MathsConf7 was delivered by Christine Andrews, Andrew Taylor and Gary Wing, and looked at the developments and questions about the new Maths A Level for AQA. This blog is just my interpretation of their workshop, and shouldn't be taken as gospel, although I've tried to reproduce accurately what was said. It's also worth remembering that these materials are still in draft form, and have not been accredited by Ofqual yet.

The session looked at many more than the titular 10 issues, and provided a lot of food for thought - I'm looking forward to teaching the new A Level, but it will be hard to mentally move away from the modular system.

Teaching and examining using the "large data set"
Many of the Statistics questions will now be based on a "large data set"; AQA have chosen Family Food, which is published by the Office for National Statistics every December. Christine clarified that this selection would not change through the lifetime of the specification, but that the updated version would be used every year, and examination questions would be set using the most recent set of data; I took this to mean that exams in summer 2018 would use data published at the end of 2016. Christine also highlighted that teaching using the data set would not be compulsory, but that familiarity with the scenarios and language used would be advantageous in an exam situation (see example below: Paper 2, Q14 from the AS Level papers, available here). This approach would certainly make the teaching of statistics more coherent, and give lots of time for real in-depth analysis of one problem, as opposed to skimming over the surface of many different scenarios. Gary highlighted the opportunities to investigate these data further using technology such as Excel and MatLab.

Peter Mattock's session at #mathsconf5 (Concrete Approaches to Abstract Mathematics) was great and gave me a lot of takeaways, so signing up for this one as my first session seemed like a no-brainer. I wasn't disappointed; this time, Peter looked in depth at fifteen topics that can lead to misleading assumptions by pupils, and challenged us to come up with examples that "broke the mould".

We started with a little game; Peter asked us to come up with examples we could use to teach particular topics, such as a solvable linear equation or a diagram for teaching parallel line properties. I could sort-of see where this was going, but I decided to embrace the task as it was designed and go for my first idea for each example. We were then awarded points for the predictability of our answers - I scored a whopping 17/20 on my first go with some completely textbook examples. Peter then asked us to improve these examples to come up with a problem set that would score zero. I've neatened up (but not censored!) and scanned my notes below, with the original example on the left and improved examples on the right.

As I promised my first #mathsconf7 blog before the en d of Monday, I thought I'd better crack on, which means turning pages of tiny scribbled notes on an old Osiris pad into something a little more coherent.

Much like @taylorda01, I've spent a lot of time in Leeds over the last decade (three years of university, followed by two years travelling up and down nearly every weekend, followed by a further five years living there and working in Yorkshire) and have never been to the Royal Armouries, but I concur with him that it worked well as a venue, and the unrelated event going on in the Leeds Dock area certainly added a bit of a party atmosphere every time I walked from New Dock Hall to the main Armouries building.

First Complete Mathematics conference of the academic year - the best yet?

Today's post is a blog about blogging - does that make it a meta-blog? 

I'll start with my fiance's reaction when I told him about the #summerblogchallenge - he was convinced that there was no way I could write 51 meaningful blog posts, and was in danger of just spamming my Twitter feed with rubbish - hence the title of this post. I think he's also concerned that I spent the first day of the summer holidays pre-writing posts and coming up with ideas rather than starting the big it's-the-summer-holidays spring clean of the tip we're currently living in. This got me thinking about what my aims are when I post, and why I do it.

When I started blogging this year, I felt a little self-conscious. There are a lot of well-established teaching blogs already out there, and I couldn't see what I could contribute. However, I'm really glad I waded in, as it's really reinvigorated my teaching this year, along with loads of other advantages. So this post is for any on-the-fence would-be bloggers who are debating wading into the blogosphere.

It arrived! Having ordered a copy of Alex Bellos's second book, Alex Through the Looking Glass right after discovering it existed on 11th February, the gods at Amazon finally decided to deposit it on my doormat this afternoon. I nearly crushed it when I opened the door...

So after hacking into it with an over-large knife (couldn't find the scissors) and discarding the packaging in a very haphazard fashion, I started reading. I've read three chapters tonight, on and off, and am going to finish Chapter 4 before I go to bed (although it does appear to be about conic sections...urrrrgh). I absolutely loved his first book (Adventures in Numberland) and have read it cover to cover at least three or four times, and dipped into it for lesson ideas (it's looking very dog-eared now) and I'm pleased to say I'm enjoying this one just as much. 

So far this evening I've discovered:

• Shakespeare is responsible for turning the mathematical word "odd" into its current meaning of "strange" or "unusual"; prior to his writing, everyone understood it in a mathematical sense only.
• Odd numbers are usually associated with more "exciting" products (Levi 501s, 7UP) while even numbers are more reliable (WD40). And interestingly, they've done studies that show that people will pay more for products depending on the numbers associated with them.
• Why lots of people have the number 7 as their lucky number.
• How Benford's Law is used to catch fraudsters and why the number 1 is the leading digit of about 30% of most data sets.
• A solution to an argument I was having with my tutor group yesterday morning about how everything is related to maths - one of them got quite upset when I showed them this as apparently I'd broken Biology forever.
• Exactly how triangulation works and why it was so useful for navigation before laser methods for measuring distances. Sadly, I discovered that there are no intact trig pillars other than church spires anywhere near my house or school, so that's that field trip idea in the bin. Despite this, I'm definitely going to show this in class the next time I teach trigonometry. You can check your local trig pillars on this lovely little site.

If you like maths books, particularly those which don't give you a headache because the maths requires you to dig out university notes to understand the first paragraph, I'm recommending this. Of course, I'm only three chapters in, and the bit on conic sections may kill me (3D geometry is not my favourite thing ever). Wish me luck!

The first session I attended at Celebration of Maths 2015 was titled "Effective Revision" and run by Ryan O'Grady (@tiredoldcliche). My colleague had picked the sessions for us, and I wasn't sure I'd get much out of this - I was pretty convinced that I'd got revision sorted. So far this year with Year 11 I've used:

• Typical past paper practice, with red/amber/green topic sheets to record their results; 
  
• The brilliant Maths Takeaway booklets from Kesh Maths (my pupils seem to really like these - I have had requests for "doing more of those topic booklets, please" from quite a few of them);
• Revision folders to collect all their past papers, posters etc as we've gone through the course;
• Creation of revision posters or cards for key topics, so all the pertinent notes are in the correct place.

However, this session made me think again about how effective that revision actually is. Many of us were using strategies similar to those above, but Ryan raised a few points that made me think twice.

1. Do we take organisation skills for granted?
We assume that pupils know how to revise and organise their time. I'm so guilty of setting the "revise for this mini-test" homework with the implicit assumption that pupils will have the slightest clue how to go about doing this. In some cases, such as those with the permanently lost maths book, they often won't have any meaningful class notes or work to revise from. I've also lost count of the number of times I've had conversations with pupils that go a bit like this:

Me: (Hands back test with less-than-adequate mark) Did you do any revision?
Pupil: Yes I did loads, like four hours!
Me: What did you do to revise?
Pupil: I read through all my notes and then went on Bitesize.
Me: Did you actually do any questions?
Pupil: No...

Despite the fact that I keep telling my pupils that they need to actually do maths to help them revise or learn, I hardly ever give them any direction to where they can find any of these resources. My direction of "use the Internet" is similarly useless - there's so much stuff around now that there's no guarantee that it will be good quality, or that pupils can even find it (MyMaths menus are an excellent example - unless you think in teacher speak, it can be very difficult to find some topics!).

Ryan suggested creating a revision notebook (preprinted with space to write examples) where pupils could record all of the really important stuff from lessons. This has obvious implications for the photocopying budget, but I wonder if it would really help certain pupils. 

2. Why don't pupils revise?
Once we've got round the organisational issues and problems, there's still the issue that some pupils just won't do revision homework (the ones that go "Yessss!" when you say that they need to revise for an assessment, because in their minds, that equals no homework). We know that revision makes a difference to final exam results, but Ryan made the important point that, for some pupils, they don't see the point in revising because they think they are still going to fail. A lot of the ideas behind this next bit come down to a pupil's mindset. A pupil who has experienced success is more likely to want to work hard at something than one who has attempted to work hard in the past but had no success (the "I'm crap at maths" bunch).

3. Working hard makes a massive difference
Combating the "I can't do maths" is one of the most difficult things to do, and I've heard it from all ages and abilities. I'm still on the fence about whether or not there is such a thing as "natural maths ability". If there is, I certainly don't have it - I was much better at French and German at school and breezed through my English Literature exams without lifting a finger, but I had to work hard at Maths. I think this is one of the reasons I came to enjoy it so much, purely because I did actually have to think during Maths lessons and didn't get bored because it was all too easy. Obviously there is some difference between "any old" maths graduate and someone like Andrew Wiles, but my personal opinion (backed up by absolutely no research or concrete evidence at all) is that most people are equally capable of doing maths, it's just that at some point on the mathematical journey, an important building block gets left out and then the cycle of desperation starts.

Sometimes pupils don't see just how important hard work in Maths is, partially because there's this culture of "either you can or you can't", and it's socially acceptable to be part of the "can't" crew. But I've had at least two pupils in the past - "bottom set kids" (with sarcastic quotation marks) achieve well above their targets of Fs and Es to get a grade C at the end of Year 11, and this was purely because they worked really hard every single lesson.

Ryan showed us one video in the session that illustrates this point beautifully - it's Ed Sheeran on Jonathan Ross's chat show, explaining just how bad he used to be at singing.

Ryan also mentioned Malcolm Gladwell's theory that you need 10000 hours work in a subject to become an expert. A little bit of Googling reveals that actually it seems to be a little less than this, which is comforting news for our pupils, but I think this is also worth sharing with them.

In a similar vein, it's worth sharing the story of Dan McLaughlin, who quit his job in 2010 to take up golfing, despite having never played a complete game in his life. He's not reached the 10000 hour mark yet, but is competing nationally. There are a few great videos on his site.

4. What motivates pupils to revise or work hard?
If pupils do revise, it is likely that they've already bought into some of the points discussed above. One thing that Ryan mentioned (that is apparently backed up by significant research - I'll have to go digging) is that extrinsic rewarding (stickers, stamps, sweets, bribery!) does very little in motivating pupils to work hard. This really stuck with me - many of our reward systems at school are based on this premise, but it kind of makes sense that frequent extrinsic rewards might diminish or mask the intrinsic reward of personal success through hard work.

Something else mentioned (which I think is the most important thing I've learned in teaching) is that pupils are most motivated by a teacher they can trust and build confidence with. I think it's important to start off building small measures of success, particularly with a new class, so when you get onto the stuff they're really going to struggle with, they don't lose complete faith that they'll never get it.

5. Using deliberate practice
Build time into lessons for pupils to deliberately practise the skills they have learned. This is something I shied away from in my first couple of years of teaching (surely every lesson needs to be whizzy with seventeen different card sorts and pupils running round the room), but I've got significantly better at it this year. Working on a mastery curriculum model (and having quite a bit of success with it!) has made me realise how important it is for pupils to practise what they have learned, sometimes over and over again until it's almost automatic. This is why my Year 9s can successfully add fractions a month after I've taught it (that's never happened before). 

Ryan showed us a couple of nice videos to illustrate this point - Odell Beckham making "the greatest catch in the history of football", and then his warmup sessions repeatedly practising exactly the same catch.

As this post seems to be going longer than I'd planned, I'm going to stop there and write Part 2 some other time. In the meantime, Ryan kindly shared the resources from the session on Twitter, so pop over for a mosey!

I have to admit, I was flagging by this point in the afternoon. A combination of an earlier-than-usual start on a Saturday and an inevitable caffeine crash and accompanying headache at about half three meant I was actually (shamefully) considering disappearing early - but I am SO glad I stuck around for Marcus du Sautoy's lecture to finish the day.

I'm a big fan of School of Hard Sums, and I love some of the TV shows that Marcus has done, so I knew this would be good. What surprised me was just how exciting it was being in a room full of enthusiastic mathematicians listening to a lecture from an enthusiastic mathematician; it's this joy that I wish we could bottle and give to students somehow. The hour flew by, and I left with a spring in my step and a reminder of why I love maths so much.

Marcus started the talk by showing us some sequences, and talking about how mathematics was about pattern-spotting. I got the first couple of sequences (I love how I turn into a school child again whenever anyone asks me a maths question and I get excited because I know the answer), but the sequence 1, 2, 4, 8, 16, ... threw me and everyone else in the audience. You'd assume the answer was 32, but it's actually 31, because this is the sequence of circle division numbers. Quite a nice illustration of how mathematical patterns can be deceptive!

Another interesting point from this is the use of the Fibonacci (why can I NEVER spell that) in music, or more accurately, the fact that the so-called "Fibonacci" sequence was being used for beat counts in Indian music way before Leonardo gave his name to it. @Kirstymaths tweeted a pic of this that's worth checking out.

Marcus then talked about prime numbers, and suggested a more intuitive reason that 1 isn't a prime number. If we think of the primes as building blocks for all the other integers (Fundemental Theorem of Arithmetic), then 1 isn't prime because we can't make anything with it. It's interesting that mathematicians have flipped back and forth on 1 for years; I vaguely remember something from my Numbers and Algebra course in the third year of my degree, but Wikipedia is much more accessible than the lecture notes gathering dust in my loft.

The lecture then progressed to talking about cicadas, insects whose life-cycle lasts a prime number of years. I remember finding out about this last year when a friend in America sent me a video very similar to this one of cicadas in his local area; I was amazed at the volume the insects create, and even more amazed when I read some of the linked news articles that explained that these particular cicadas emerge once every 17 years. There are some theories that this is to do with the cycles of now-extinct predators; choosing a prime numbered life cycle would mean that the cicada has less chance of meeting a surge of predators whose life cycle works on multiples of 2 or 4 (for example). I've also just found a nice video from the BBC's Life in the Undergrowth narrated by David Attenborough - I'm feeling inspiration for a lesson on primes and LCM here!

We then did a lottery activity, and Marcus predicted (pretty accurately) how many of us would have 1, 2 3 or 4 numbers correct. He talked about the ideas that people don't select consecutive numbers because they think these are less likely, but pointed out that half of all possible choices contain consecutive numbers. He also talked about the 1, 2, 3, 4, 5, 6 selection - I love using this when I do combinations with Year 12, and having a discussion about how you think you're clever because (if you're a mathematician) you know that this is equally as likely as any other possible combination, but how you'd be kicking yourself if you won, as there are (apparently) about ten thousand people in the country who pick this per week, and you'd be splitting the prize more than if you went for 22, 23, 24, 25, 26, 27.

Marcus finished with a lovely demonstration of patterns in populations, looking at one model for lemmings to explain the four-year "suicide". Thanks to QI (about 20 minutes in, profanity warning), I was already pretty clued up on the lemming myth (another proud schoolkid moment!), but Marcus demonstrated (using quite a simple mathematical model) how a population could stabilise, then changed this model to show how the lemming population could vary wildly to explain the four-year dip. Again, tempted to try this in the classroom!

I'm sure there's lots of stuff I've missed, but this was a brilliant way to end the day. Like I said at the start, there's something infectious about being in a room full of people who love maths and are enjoying themselves doing or thinking about mathematics, and it's a shame that this doesn't translate to our students sometimes. 

I've been using bar modelling quite extensively in my teaching since being involved with the NCETM's multiplicative reasoning project last year. Part of the project was to emphasise the importance of diagrammatic representations of problems in teaching maths for understanding; we were given materials to deliver to Key Stage 3 classes, some of which included use of Singapore bar modelling for topics such as fractions, percentages and ratio. I found the work we did really altered my teaching; I think that I managed to teach addition of fractions successfully for the first time since I started teaching, and I was amazed at just how well my students retained efficiency and accuracy with "traditional" written methods.

It seemed like a bit of a no-brainer to pick the bar modelling workshop at the Celebration of Maths, so I and my colleagues trotted along to the session, sat down with our mini-whiteboards and got ready to draw some bars. One thing I was really keen to get out of this session was to iron out some issues I still had with using the bar to solve problems with negative amounts, and I was still struggling to see how to apply bar modelling to exam technique (see my attempt with the Edexcel SAMs here).

First of all we looked at some simple problems, like fractions of amounts. I'm already pretty happy with this - there are plenty of examples of stuff like this in my Year 7's books at the moment. I was so proud of myself that I thought I'd add a really constructive "what went well" to my work too.