#MathsConf13 took place last Saturday, and as usual, was another fantastic day of cheap CPD. Sadly, I missed the London conference in the summer, so I was really looking forward to this one. It definitely didn't disappoint, despite being a bit of a struggle at nearly 8 months pregnant!

One highlight of the day was the keynote from Matt Parker; I have to confess to spending the first few minutes wondering why this bloke looked so familiar until I realised that I'd seen him in the superb Numberphile videos.  He was highly entertaining, but also gave a few decent ideas for use in the classroom, such as thinking about images as RGB spreadsheets and creating a mega-Menger sponge or a fractal Christmas tree.

My three speed-dates were as follows:

• Catching up with a colleague from my old school - I know, this isn't really what speed dating is for, but we did have a good chat about their decisions regarding GCSEs and A Levels!
• Paul (@PaulRodrigo2718 ), who showed me his method for scaffolding problem-solving questions at GCSE.
• Richard (@TickTockMaths), who shared the absolutely superb dudamath.com, which I'd not seen before but has so much going on that its potential for use in the classroom seems massive.

Rather than attempting to blog about each workshop (I still haven't finished my #mathsconf7 round-up - now unlikely to ever happen!), I decided to make the most of my time off by doing a bit of relaxing colouring-in - so this conference's workshop posts are in "visual blog" format. I attended:

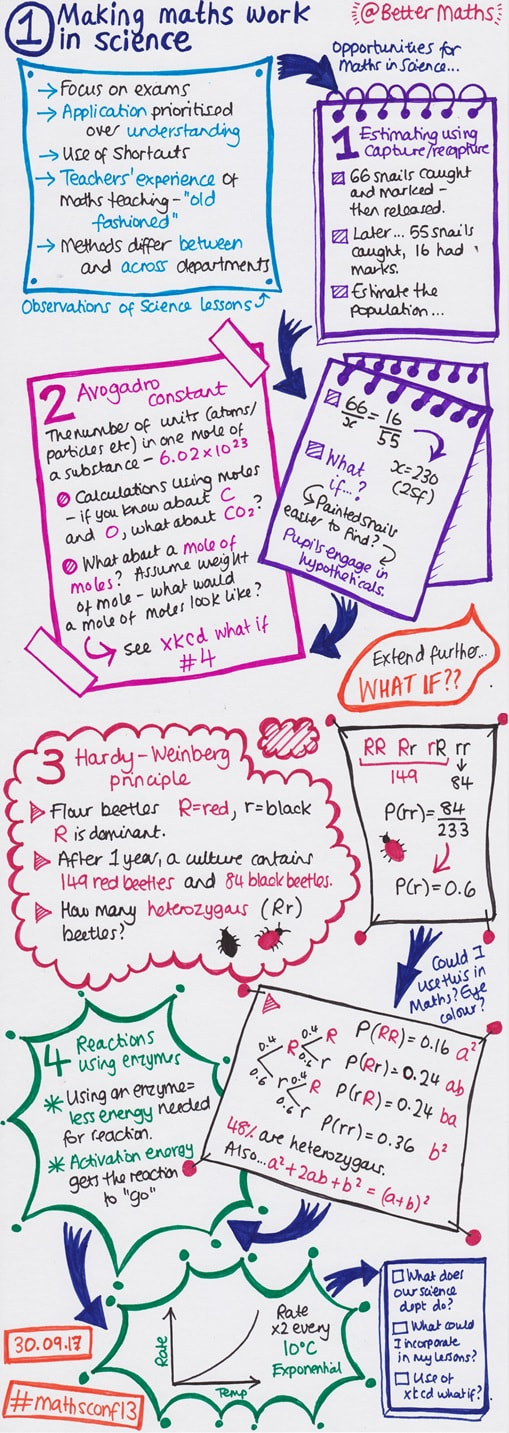
1. Making Maths Work in Science with Luke Graham (@BetterMaths);
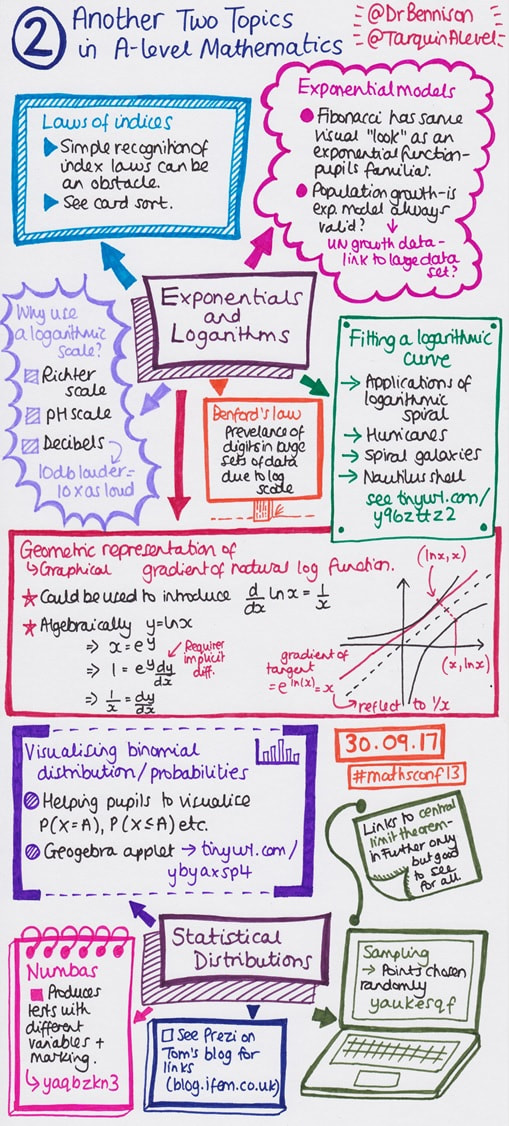
2. Another Two Topics in A Level Mathematics with Tom Bennison (@DrBennison) and Ed Hall (@TarquinAlevel);
3. Things to Do With your Large Data Set with Stella Dudzic;
4. Problem Solving - Getting to Grips with the Overarching Theme 2 in the New Maths A-level with Dan Rogan.

The Prezi from the session and links to all of the applets and resources mentioned can be found on Tom's blog post.

Session 2 at #MathsConf7 was delivered by Christine Andrews, Andrew Taylor and Gary Wing, and looked at the developments and questions about the new Maths A Level for AQA. This blog is just my interpretation of their workshop, and shouldn't be taken as gospel, although I've tried to reproduce accurately what was said. It's also worth remembering that these materials are still in draft form, and have not been accredited by Ofqual yet.

The session looked at many more than the titular 10 issues, and provided a lot of food for thought - I'm looking forward to teaching the new A Level, but it will be hard to mentally move away from the modular system.

Teaching and examining using the "large data set"
Many of the Statistics questions will now be based on a "large data set"; AQA have chosen Family Food, which is published by the Office for National Statistics every December. Christine clarified that this selection would not change through the lifetime of the specification, but that the updated version would be used every year, and examination questions would be set using the most recent set of data; I took this to mean that exams in summer 2018 would use data published at the end of 2016. Christine also highlighted that teaching using the data set would not be compulsory, but that familiarity with the scenarios and language used would be advantageous in an exam situation (see example below: Paper 2, Q14 from the AS Level papers, available here). This approach would certainly make the teaching of statistics more coherent, and give lots of time for real in-depth analysis of one problem, as opposed to skimming over the surface of many different scenarios. Gary highlighted the opportunities to investigate these data further using technology such as Excel and MatLab.

When I was younger, I was ridiculously cynical about Valentine's Day - I'd wonder why people needed one special day to tell or show their significant other how much they love them, when surely that should be happening all the time. However, as I'm often working late into the evenings (I get in at 4pm but usually do 2-3 hours at home in the evening), sometimes I find my husband's come in at 5 and I've not even acknowledged him, because I'm so engrossed in school-work. It's very easy to neglect to remind the people who are important to you just how important they are - family and friends as well as significant others.

If you haven't heard of xkcd (click now and lose three hours), it's a webcomic run by Randall Monroe focusing on maths, science and computing. Although some of his comics (mostly the coding ones) go over my head, the maths-based ones are hilarious, and some are great for sharing in lessons - with the caveat that some do contain naughty jokes, so check first. Here's my pick of a few particularly relevant to the A Level syllabus: