So far this evening I've discovered:
- Shakespeare is responsible for turning the mathematical word "odd" into its current meaning of "strange" or "unusual"; prior to his writing, everyone understood it in a mathematical sense only.
- Odd numbers are usually associated with more "exciting" products (Levi 501s, 7UP) while even numbers are more reliable (WD40). And interestingly, they've done studies that show that people will pay more for products depending on the numbers associated with them.
- Why lots of people have the number 7 as their lucky number.
- How Benford's Law is used to catch fraudsters and why the number 1 is the leading digit of about 30% of most data sets.
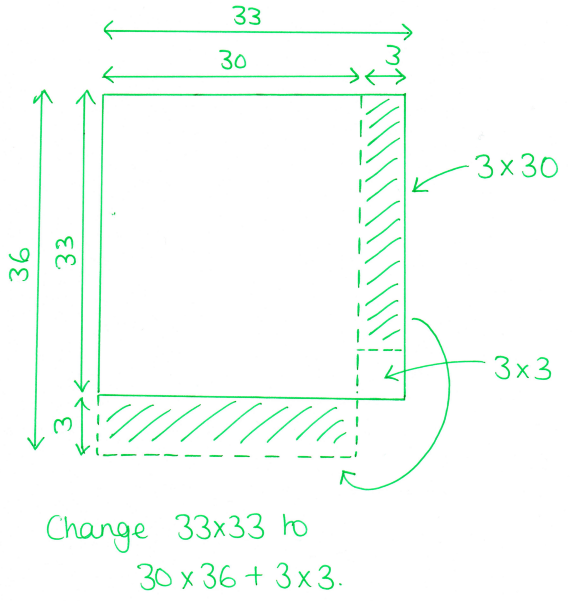
- A solution to an argument I was having with my tutor group yesterday morning about how everything is related to maths - one of them got quite upset when I showed them this as apparently I'd broken Biology forever.
- Exactly how triangulation works and why it was so useful for navigation before laser methods for measuring distances. Sadly, I discovered that there are no intact trig pillars other than church spires anywhere near my house or school, so that's that field trip idea in the bin. Despite this, I'm definitely going to show this in class the next time I teach trigonometry. You can check your local trig pillars on this lovely little site.
If you like maths books, particularly those which don't give you a headache because the maths requires you to dig out university notes to understand the first paragraph, I'm recommending this. Of course, I'm only three chapters in, and the bit on conic sections may kill me (3D geometry is not my favourite thing ever). Wish me luck!

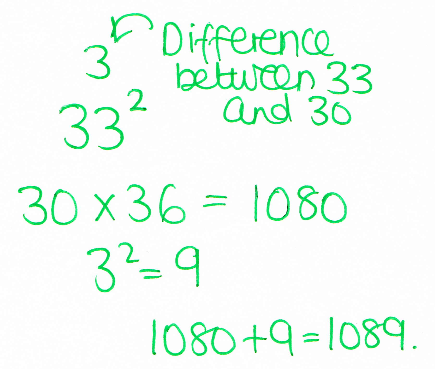
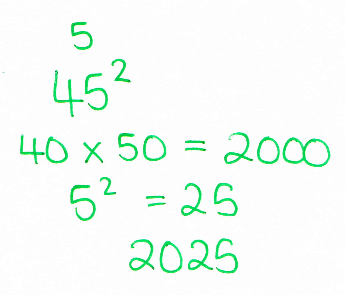
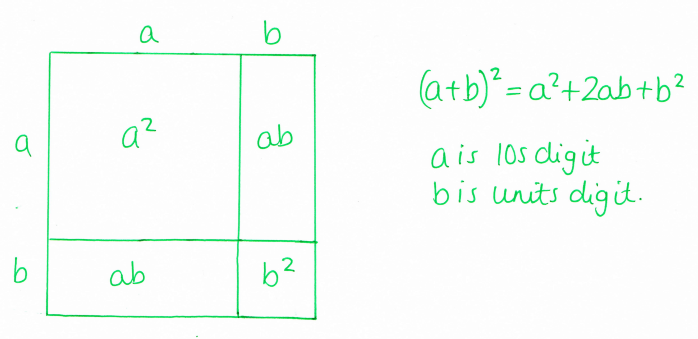



 RSS Feed
RSS Feed
