LOTW 10/05/15 - Comparing and ordering fractions and decimals

In the spirit of encouraging personal positive thinking, I've decided to start a new Sunday blog series on the best lesson I've taught the previous week.

This week my pick actually covers two lessons of work, and was delivered to my Year 9s on Thursday and Friday. To provide a bit of context, we're trialling the Mastery Pathway with KS3 this year, and pupils sat the Elementary 4 test on Tuesday, covering negative numbers, substitution and lots of fractions and decimals work. They passed the previous three tests pretty well, but this one caused some difficulties, with marks ranging from 30% to 70%. After doing a bit of analysis on the results, I decided that my first topic for re-teaching would be working with fractions and decimals, particularly ordering and converting between the two representations.

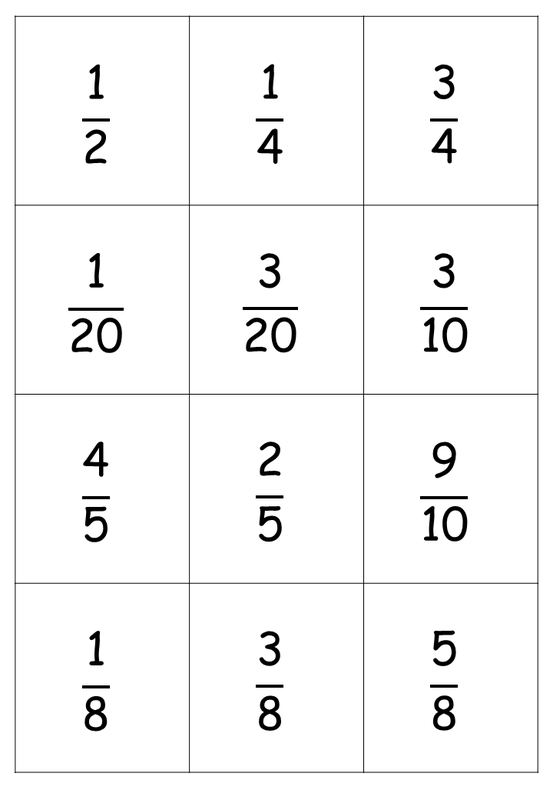
I'd tried theStandards Unit card sort with them a couple of weeks ago, and that didn't really work for them - although they had a good go, it was too overwhelming for them. I decided to adapt it slightly, removing the percentage cards (we've not covered percentages at all yet in the Mastery Pathway), and changing the denominators to something slightly more friendly. I also added significantly more structure to the activity, interleaving skills practice with the card sort. The adapted version worked really well, and I'm pretty confident that I've plugged most of the gaps with most of them now - I'm planning a quick test next week to check.

• Download this resource
• Find out about password access

---

1. Ordering fractions using a common denominator

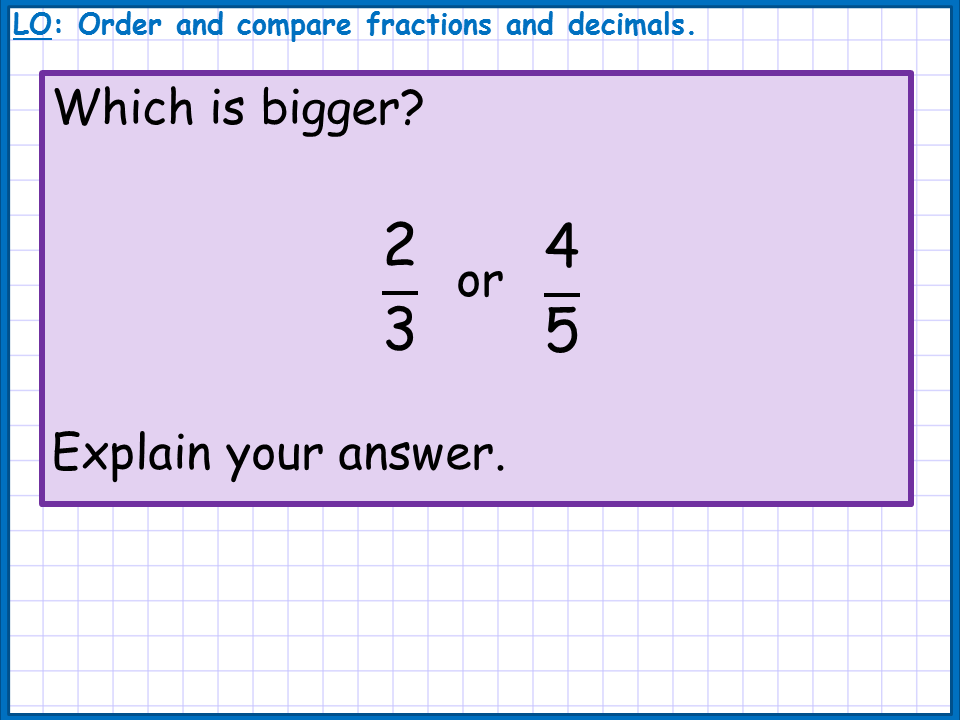
We started with a "which is bigger" problem - I've previously blogged about how much I love this activity, and we did a lot of work at the start of the year with problems like these.

It was really positive to see that their mathematical explanations have come on leaps and bounds since the start of Year 9. We discussed the ideas of using a common denominator and pros and cons of bar and pizza modelling again. 

I then gave them four fairly standard problems to do. We discussed the importance of showing working out - on the test, many of them hadn't shown their working, and had lost method marks. I asked them all to show clearly which common denominator they had used and how they converted the fractions.

I deliberately picked the fourth problem with a common denominator of 100, to lead us into the next bit on converting fractions to decimals.

Next, I handed out a set of fractions cards from the card sort I planned to use. I asked what they would pick as a common denominator for the nine fractions highlighted, and got the pupil who said "twentieths" to explain why. 

We also discussed what they would use as a common denominator for the whole set, and how they could find this. However, I wanted to focus on the twentieths to start with, so I got them to convert those, writing their answers on the cards.

---

2. Converting fractions to decimals

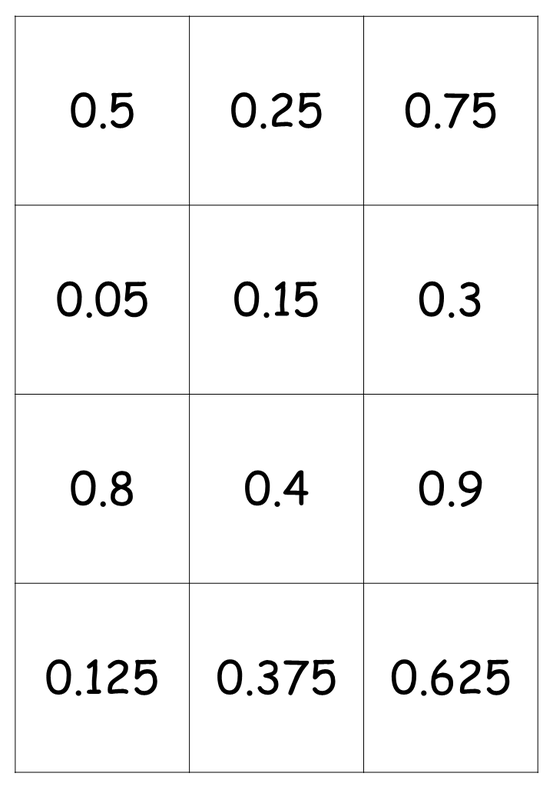
I then quickly retaught conversion of fractions to decimals with "easy" denominators. I was confident that they understood the concept and links with place value, as we spent quite a bit of time on this when I initially taught the topic, but they clearly hadn't mastered it as many of them made errors with this on their assessment. We discussed a few examples, then I set them off with ten to do for themselves.

We spent a couple of minutes discussing different strategies for the final question, and I got two pupils to the board to demonstrate their alternative approaches: converting to a mixed number, then dealing with the fraction part, or converting to a denominator of 100 first, then converting to a mixed number.

The pupils then changed the first nine fractions into decimals using a denominator of 10 or 100. We discussed why the eighths might cause problems, and suggested that we could use a denominator of 1000. However, as I wanted them to try these using division, we didn't change these too at this stage.

Next, we did a quick refresher on dealing with more difficult denominators using division. On their tests, many pupils had confused the numerator and denominator, with many instinctively putting the larger number under the "bus stop" and then getting in a mess. 

We talked about the fact that order matters with division - as an aside, I've stopped automatically correcting pupils when they say this the wrong way round, and instead asking them if they're sure they mean "9 shared by 45" instead of "45 shared by 9". I also reinforced correct use of recurring notation.

Finally, I got them to change the eighths cards using division. By this point, we'd reached the end of the first hour, so we quickly summarised to pick up where we'd finished off the previous lesson.

---

3. Converting decimals to fractions

We sped through this bit, as we covered this in lots of depth during Elementary 1. My main focus here was getting pupils to simplify their answers, particularly with a factor of 5 in the numerator and denominator, so I included plenty of examples of this type.

While they were doing these ten problems, I circulated to check they were cancelling down their final answers - often, all that was needed was a quick "point" at their page to prompt them to check again!

---

4. Putting it all together

For the remainder of the lesson, I got pupils to make a summary poster of all the work we'd done, using the cards we'd worked on in the previous lesson. They drew a number line on a sheet of A3 paper, and ordered the twentieths cards, then matched up the decimal equivalents. We used the decimal equivalents of eighths to position these on the number line, then I demonstrated checking this by converting all the fractions to eightieths.  

I'll add some pictures of the finished posters tomorrow.

---

Evaluation and final thoughts
This lesson is a lot more "I do, then you do" than most of my lessons, but it seemed to work really well for the pupils. Most of them found it a real confidence booster, and enjoyed the opportunity to just reinforce skills they were shaky on. They found the card sort much more accessible with a step-by-step approach. I'd use this again next year with a similar group, possibly adding a few extra cards for fractions greater than 1.

---