Teaching trigonometry (1)

I've been teaching trigonometry from scratch with Year 10 this week, so thought it would be a good opportunity to blog about the way I introduce sine, cosine and tangent. This is another sequence of lessons I love teaching, because it's one of my tried and tested approaches and seems to work well each year.

​We started the lesson with a few quick questions on Pythagoras' theorem (I used these ones). I taught them Pythagoras' theorem way back in November, but most of them remembered how to solve the problems with a bit of prompting. I was aiming to refresh identification and use of the word "hypotenuse" and also provide a link from something they'd previously learned about right-angled triangles. After we'd done this, it was on to the first bit of the trigonometry introduction!

---

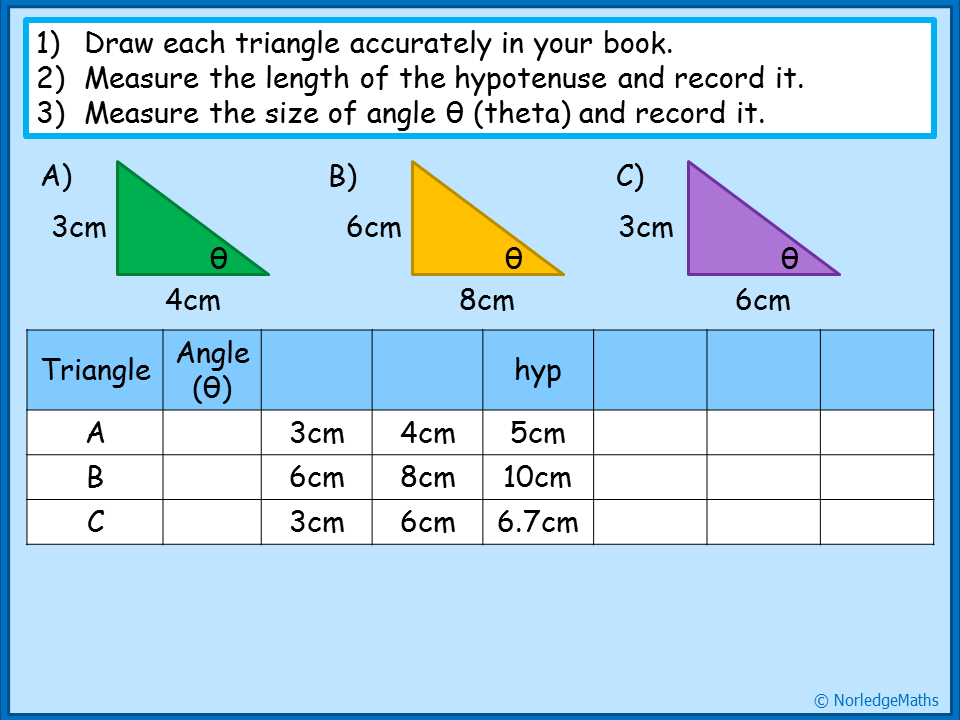
1. The relationship between lengths and angles
After trying a few different approaches in my first few years of teaching, I've settled on introducing trigonometry by drawing and measuring triangles. When I taught this initially, I used three nested similar triangles, but I found that this caused confusion for some pupils, as they couldn't see the three separate triangles clearly. I adapted this to look at the triangles separately last year (see this video on YouTube if you're interested in a tutorial for pupils to follow), but I decided to try two similar and one different this year. 

I asked the pupils to draw the three triangles in their exercise books, measure the length of the hypotenuse and angle theta and record their results. Next I introduced "opposite" and "adjacent" terminology and we added those column headings to their table. I then got them to calculate opp/hyp, adj/hyp and opp/adj using calculators and add their results to the table.

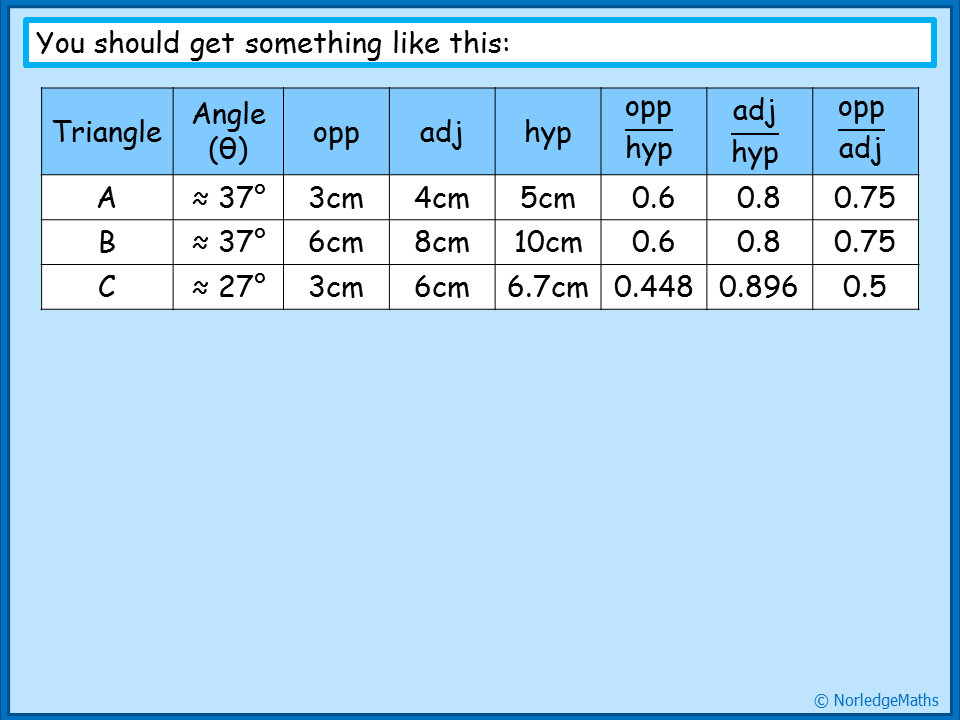
We discussed what we saw from the results; why were the results for triangles A and B identical, but the results for C were different? We got to the idea that there was a link between the side measurements and the angle we'd measured, and that if the triangle was enlarged, both the angle and the ratio of the measurements would stay the same.

• Download this resource
  
• Find out about password access

---

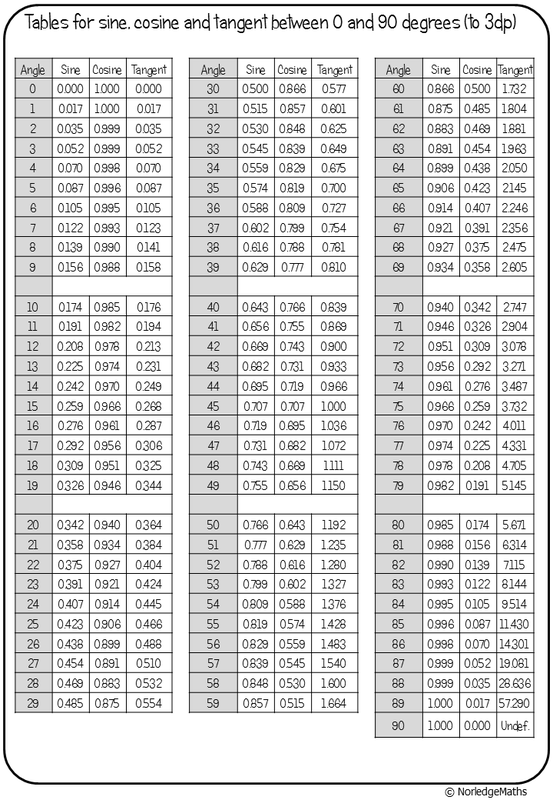
2. Using trig tables
When I first tried this way of introducing trigonometry, I got pupils to then work out sine, cosine and tangent of the angles on their calculators, and spot that these came out with the same results, moving quite quickly on to missing angle problems the same lesson. However, in the last couple of years, I've avoided calculators altogether for the first lesson or two, and got pupils using trig tables instead. 

So after the activity above, I handed out a set of trig tables (download a copy here) and got them to look at the rows corresponding to the angles in their triangles. We spotted that our results matched fairly well with the values in the tables, and discussed how inaccuracy in measurements could have contributed to our results being slightly out.

By this point we were reaching the end of the lesson, so to finish off, I taught them the names of the three ratios, emphasising that these are just relationships between two sides on a right-angled triangle (for now!).

---

3. Writing sine, cosine and tangent ratios
After a few more Pythagoras problems to kick the lesson off, I set the pupils off on a task focused on labeling sides and writing trigonometric ratios correctly. I gave them a set of triangles with all three side lengths shown and asked them to write down the ratios for sine, cosine and tangent for each triangle. Once they'd done this, they worked out the decimal values of each one on their calculators, then it was back to the trig tables to work out an approximate value for the angle.

---

4. Traditional GCSE problems
By this time, they were getting a bit fed up with the tables; a couple of them were complaining that their eyes were going funny from squinting at the values, and one pupil said "but surely we don't get this in the exam?". So at this point I showed them three examples of some more traditional exam-type problems (with two sides and a missing angle), and also demonstrated how they could use the inverse sine, cosine and tangent buttons on their calculators rather than struggling with the tables, explaining that the inverse buttons were just working backwards from the trigonometric ratio to the angle. The rest of the lesson was spent practising these new skills using questions from a textbook.

(I almost felt the need to write an apology there for referring to textbook use, then stopped myself. I think it's absolutely vital that time is built into maths lessons for skills practice, and sometimes the best way to do that is to get them to work through some carefully selected problems independently).

I'll blog next week about where we go from here. I'm in two minds about continuing to finding missing sides (which is what I'd usually do), or alternatively doing more in-depth problem solving using angles first - but I've got a few days to think about it!

---