|
The very first impasse that the Zoombinis tackle is the Allergic Cliffs . Much like most puzzles in the game, the object is to get the Zoombinis across or through some physical feature in the landscape - in this case, a massive gulf between two cliffs, straddled by two rickety rope bridges. The "faces" on each cliff are "allergic" to specific features - such as sneezing when a Zoombini with rollerblades tries to pass over it.
|
- observation
- forming and testing theories
- forming sets
- using evidence
- logical reasoning
Important skills such as theory testing and logical reasoning are particularly difficult to teach or assess explicitly, but, whether due to increase in age or teaching experience since I last played this game, I found myself much more aware that I was creating and testing hypotheses almost subconsciously by seeking out Zoombinis with similar features to allow me to work out if it was red noses or rollerskates that was causing rejections.
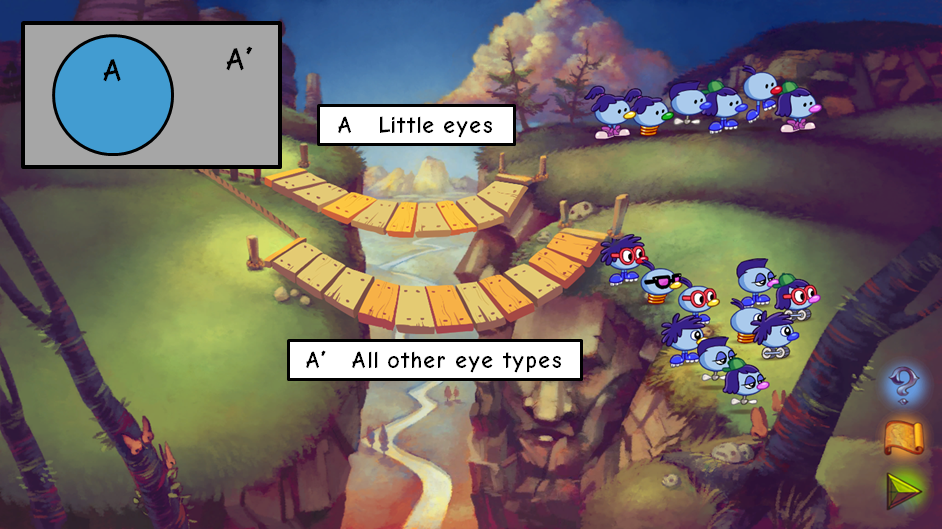
On the first level of difficulty, one cliff is allergic to one particular feature - in the example below, the bottom cliff is allergic to "little" eyes. If we consider the set A being 'all Zoombinis with little eyes', then the Zoombinis that pass over the top bridge are all members of that set, while the Zoombinis that pass over the bottom bridge are members of the set 'not A' - in other words, Zoombinis that don't have little eyes. This nicely illustrates the concepts of a set, its absolute complement and theassociated complement laws.
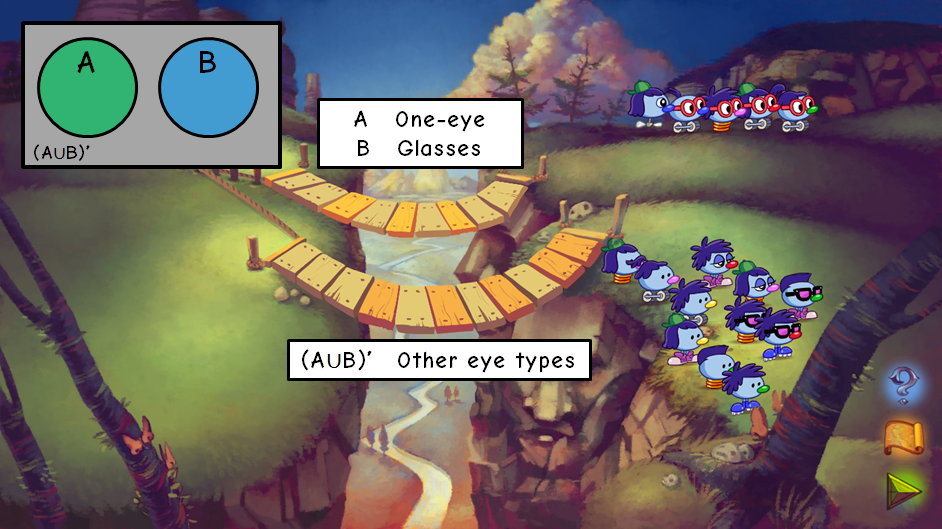
Kicking up the difficulty a notch, we then introduce another characteristic for set formation. Now, one cliff will accept Zoombinis with one of two characteristics from one type - in the example below, the top cliff only accepted Zoombinis with either one eye or glasses, while the other three eye types travelled across the bottom bridge.
We've now got two distinct sets, demonstrating the idea of mutual exclusivity; Zoombinis can have either one eye or glasses, and not both - hence there is no intersection in the Venn diagram.
The next difficulty level introduces set intersections, and immediately gets much more challenging - depending on the luck of your first few guesses, you can end up a few lives down before managing to form any workable theories.
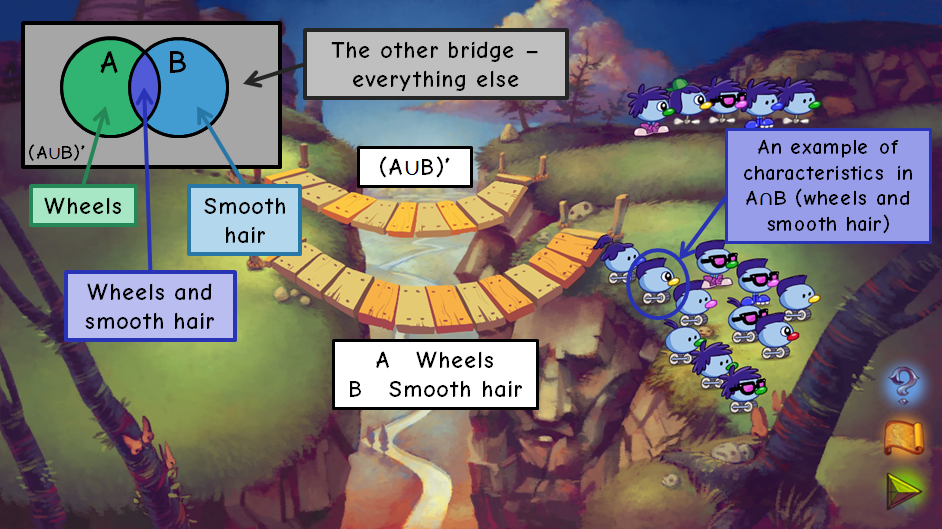
In a similar vein to Oh So Hard, one cliff still accepts Zoombinis with one of two characteristics, but now these characteristics are selected from different types - such as wheels and smooth hair in the example below. As far as I can tell, it's always the case that the features are selected from two different types, otherwise we'd be back to the previous level of difficulty.
There's a lot of interesting set-theoretic ideas here too - quite a few Zoombinis that passed over the bottom bridge had smooth hair and glasses, which places them in the dark blue intersection area on the Venn diagram.
This took me forever to get my head around, and a bit of swift Googling indicates that, by the time you get on to Very Very Hard mode with a fairly varied group of Zoombinis, there's no workable algorithmic approach to ensure success every time.
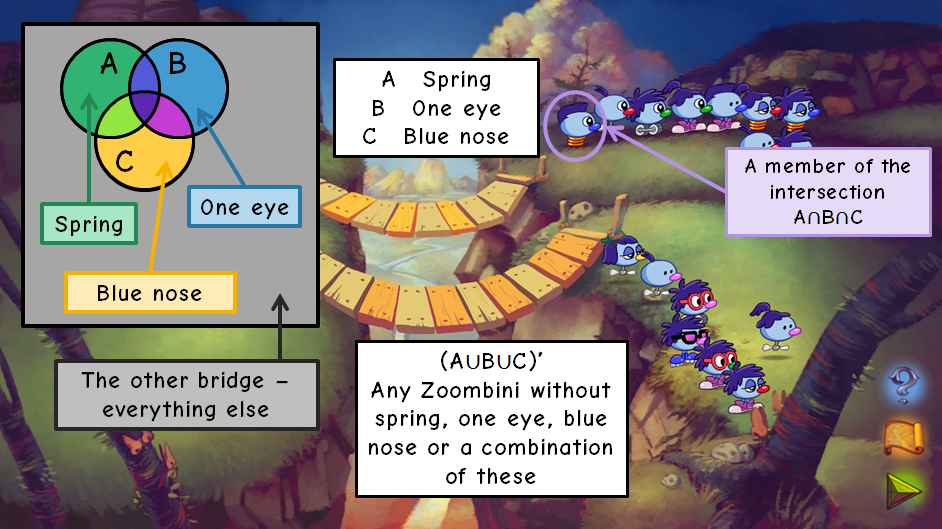
The tweak from Very Hard to Very Very Hard is conceptually simple - it's just an additional characteristic added to the list of "acceptable" ones, and again, as far as I can tell, these characteristics will all be picked from different characteristic types. In my example, the top cliff was allergic to all Zoombinis except those with either a spring, one eye, a blue nose or any combination of these features.
In some cases, it's not easy to spot the three sets even once the puzzle is complete. I had several run-throughs on practice mode, mostly because I spent the first ones losing spectacularly, but then because I was unable to categorically identify the three sets from the completed puzzle. I was pretty pleased with this final one, because not only are the sets pretty visible, but there's also a little chap that lies in the intersection of all three sets, as he has a spring, one eye and a blue nose.
- Complete the puzzle as a class on interactive board, getting pupils to make their reasoning and hypotheses explicit.
- Screenshot completed puzzles and ask pupils to identify where particular Zoombinis would fit in each Venn diagram.
- Screenshot completed puzzle and ask pupils to identify the sets or rules - this is incredibly challenging for a random group of Zoombinis on Very Very Hard mode.

 RSS Feed
RSS Feed
