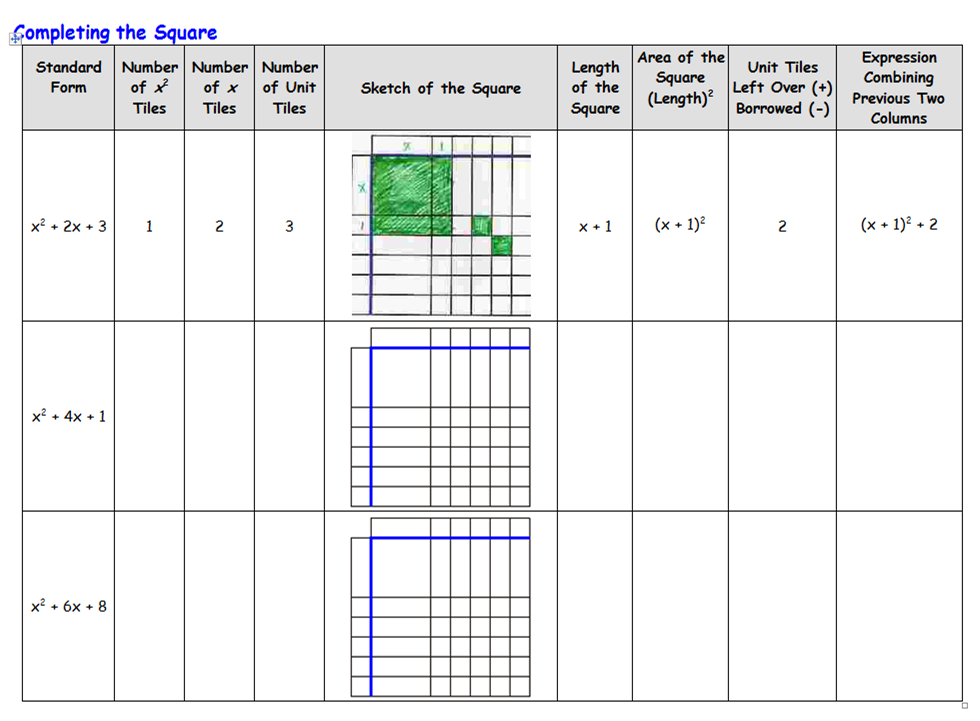
| I'd previously completely failed and confused them all by doing it via "the formula", and was beginning to wonder if I'd ever manage to teach it properly, a problem compounded by the fact that (if I'm honest), I don't think I'd ever properly understood why it worked. Anyway, I found an absolute gem of a worksheet - I've just tried looking now and for the life of me I can't locate it anywhere on Google, especially as algebra tiles really seem to have taken off in the maths education world and there's a huge stack of resources out there now. Luckily I've got a copy saved - it looked like this: |
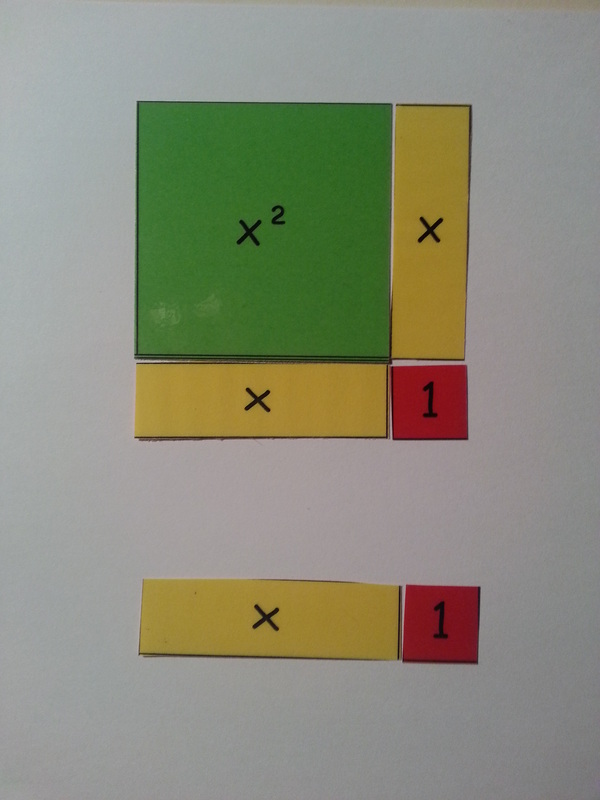
(As an aside to this, I had at least five or six pupils who continued to use diagrams to solve CTS all the way through the GCSE course. When a question came up on the exam paper, guess which pupils got it correct?)
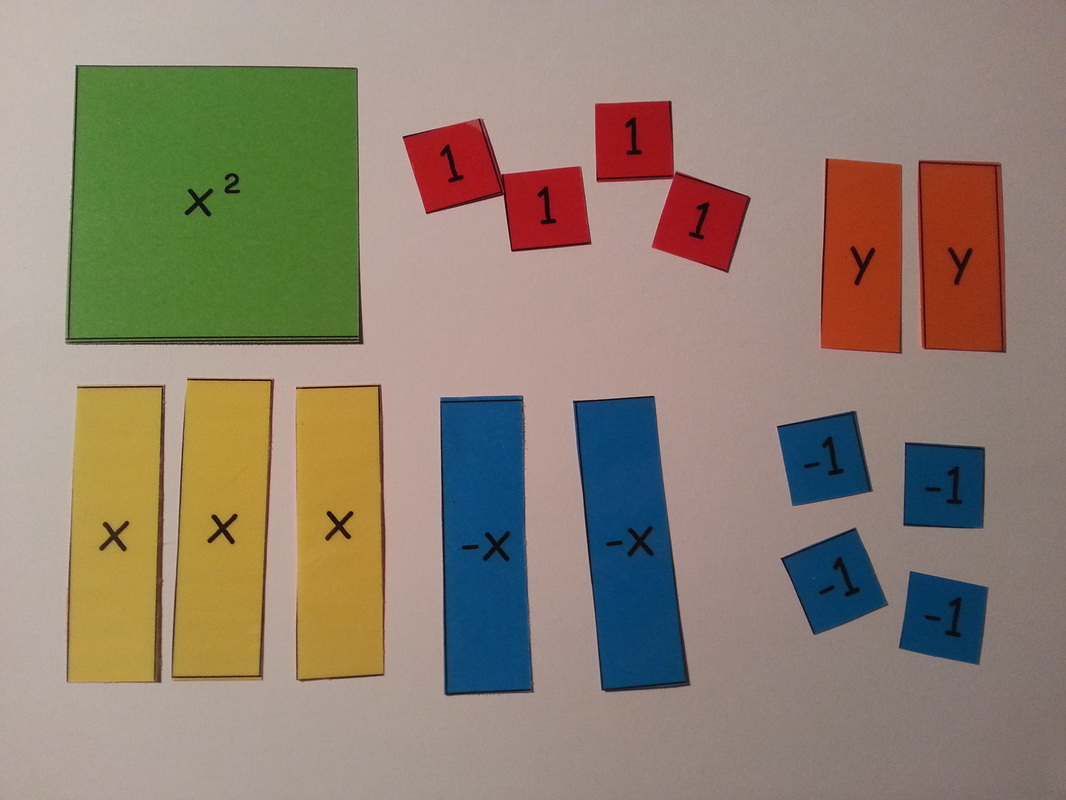
Feeling quite pleased with myself, I popped back to the Internet for a bit more research and discovered that, although pretty scarce last year, algebra tiles were actually a "thing". They appeared to be more popular in America than over here. I then spent a happy evening or two laminating and cutting out to produce my own sets of algebra tiles:
I then got some long-suffering TAs to make whole-class sets for our store cupboard, and although I've not got them out much this year (mastery curriculum with lower-attainers means a lot of fractions and multiplication and not much algebra - yet!), some of the rest of my department have used them and loved them.
The only thing I'm not entirely convinced on is using negative tiles. In a similar vein to the issues I had with bar modelling to solve equations with negatives, representing a negative quantity with a positive area can be a bit of a conceptual headache. For now, I'm sitting on the fence as to whether I'd continue to use the negative tiles with pupils, but the positive ones are absolutely essential for providing a concrete model for any algebra skills.
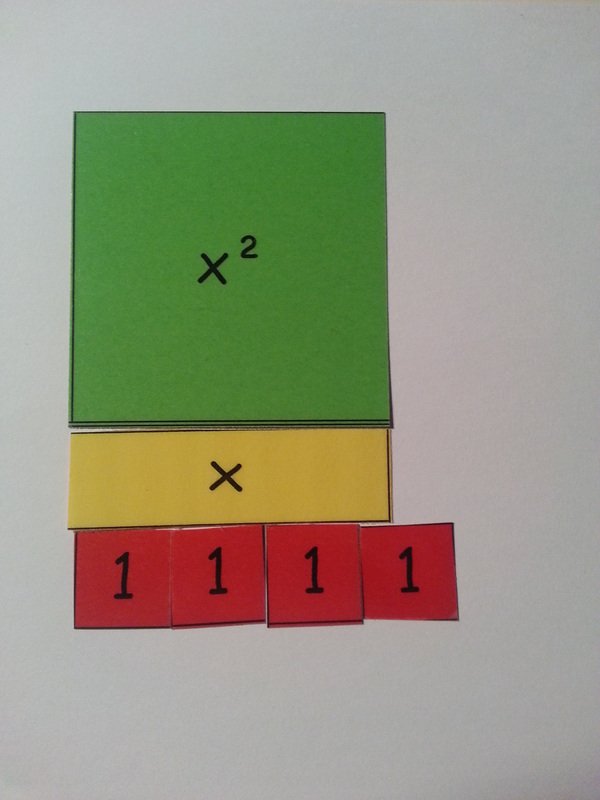
If you want to make your own, it's important to get the dimensions right. Start with a 1 x 1 tile. The x tile needs to have the same width as the 1 x 1 tile, but it's important that you can't fit an exact multiple of the 1 x 1 tile along its length - this is to stop pupils automatically assuming that x = 3 and avoid issues when factorising. The x² tile has the same length and width as the x tile (so x multiplied by x gives an area of x².
 RSS Feed
RSS Feed

Check out our algebra tiles, www.assessmentservices-edu.com/Algebra-tiles.aspx
I'd continue to use the negative tiles with pupils, but the positive ones are absolutely essential for providing a concrete model for any algebra skills.