Lesson 1 - Developing understanding using pie charts
The lesson begins with an explanation about a school canteen worker who wants to ensure that she is buying the right amounts of different types of fruit and vegetables to cater for the pupils in her school, so she surveys them about their favourite types of fruit and veg. After a few minutes of discussion around this, I then explain to pupils that we are going to do the same thing, and find out what our results look like. I did this last week with Year 7, so I'll use their results for illustration purposes.
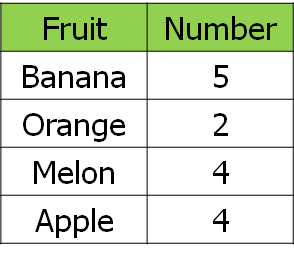
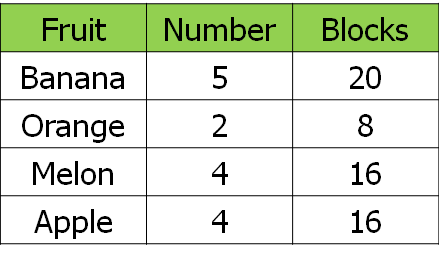
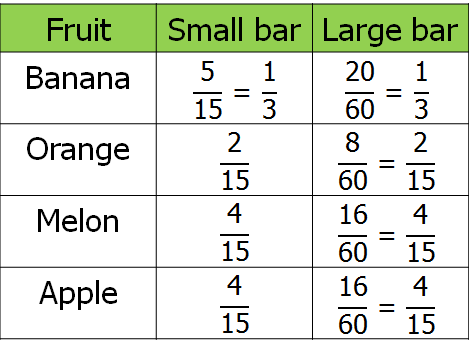
First of all, I got them to vote for their favourite fruit. It's worth "fiddling" the results a little bit here to give a useful denominator - I added myself into the survey so that we were working with fifteenths rather than fourteenths, as I wanted to get away from the idea that simplifying fractions only involves continual halving. Here are our results:







 RSS Feed
RSS Feed

Your way of introducing fraction arithmetic is very detailed. I can say your knowledge about fractions is very profound and your way of teaching is excellent. Your post is very helpful for the students to learn about fractions. They must be very lucky to have you as their teacher because you are in a different level. I also want to share my idea on dealing with fractions.
To add and subtract fractions successfully is to make the rules stick to your memory.
Rules are:
Same denominator:
Add both numerators then reduce. The result would be the final answer.
Different denominator (4 steps):
1. Multiply the numerator of first fraction to the denominator of second fraction. The result is the new numerator of first fraction.
2. Multiply the numerator of the second fraction to the denominator of first fraction. The result is the new numerator of second fraction.
3. Multiply both denominators. The result is the common denominator for two fractions.
4. Add the two new numerators. The result is the answer.
To make it stick to your memory:
Rules for subtraction:
Same denominator:
Subtract second numerator from first then reduce. The result would be the final answer.
Different denominator (4 steps):
1. Multiply the numerator of first fraction to the denominator of second fraction. The result is the new numerator of first fraction.
2. Multiply the numerator of the second fraction to the denominator of first fraction. The result is the new numerator of second fraction.
3. Multiply both denominators. The result is the common denominator for two fractions.
4. Subtract new second numerator from first new numerator. The result is now the answer.
To make it stick to your memory:
Same numerator:
Add two fractions 50 times.
Subtract two fractions 50 times.
Different denominator:
Add two fractions 100 times.
Subtract two fractions 100 times.
To check if your answer is right and your step by step solution is correct:
Use fraction calculator with button from http://www.fractioncalc.com. It is important that you follow the correct steps in adding unlike fraction. Unlike fractions are those fractions with different denominator.
The key here is to make the rules implanted into the minds of the students so that they will never forget.
It is hard to solve fraction without a thorough understanding of basic fraction. This is so true even in the higher grade levels. Student should understand first how to add, subtract, multiply, and divide fractions. They should have a deep understanding of LCM so that they can decide when to use it or not. They should also have the understanding of equivalent fractions, mixed fraction, and improper fractions. By having a depth understanding, student may find it easy and even fun to deal with fractions.
Thank you so much for sharing this post on how to add add subtract fractions. You have explained it in a very detailed manner. I have been searching reading a lot of ways to add and subtract fractions and encountered only two ways. First is you used the LCM. This is best for smaller fractions. The other is to use butterfly method where you have to cross multiply the fractions. This method is best for bigger fractions and those that has no LCM. Again thanks for sharing for this valuable information.