I'm approaching this from the point of view of pupils aiming for a grade C, as I've had borderline groups for the last two years, and no top GCSE sets for about four, due to having plenty of A Level Maths on my timetable already, so I'll admit that my pedagogy and knowledge of grade A/A* topics at GCSE is fairly limited.
Q1b - Percentage from a Stem and Leaf diagram
I'm still pretty convinced on dealing with fraction to percentage conversions with ratio tables, but I can see that it might be a little unnecessary here. I'd like to think that once pupils had got the fraction 3/20, they would spot that 20 goes into 100 five times and multiply the numerator accordingly.
Q4 - Plant Comparisons
Q9 - John's Conference
Q10 - Mary's Conservatory
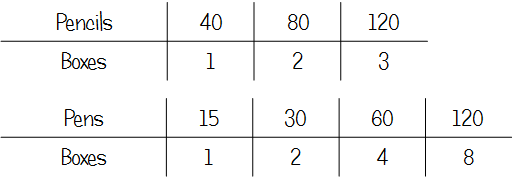
In a similar vein to the plant comparison question, the only benefit of a ratio table here is structuring working out - I don't think it adds anything in terms of making the calculation more straightforward.
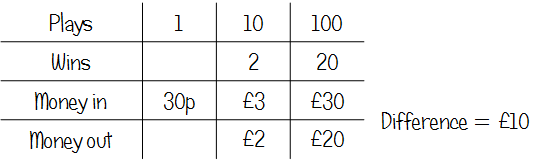
Q11 - Karl's Game
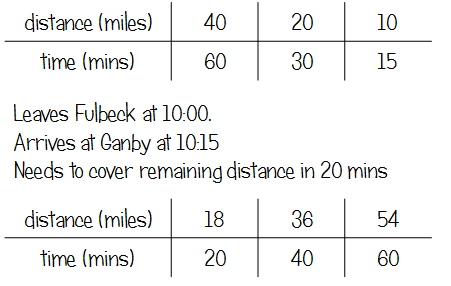
Q14 - Raksha's Journey
Q15b - Does this point lie on the line?
|
According to this site, it's a new topic coming to Foundation and Higher, so there are obvious implications for teaching next year.
Chatting to a few pupils in top sets, many of them either found the gradient, then substituted in one point to find the y-intercept, or, overwhelmingly, used a sketch. A colleague suggested that the approach she had used was getting them to work out the gradient from the two points, then work out if the third point gave the same gradient. However, I started to think about making this question accessible for borderline pupils who (let's face it) won't have as developed algebra skills as those aiming for As or A*s. |
|
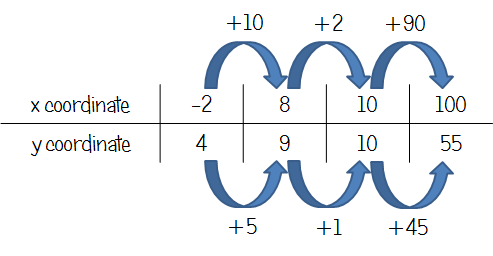
Now, obviously this isn't really a "ratio" table, as we've got a linear relationship, not direct proportion. However, if we look at the change in x and change in y for the two points we've been given, it's clear that the increase in x is double the increase in y.
From here, it's not too difficult to get from 8 to 10 and then 10 to 100 with the x coordinates, resulting in a y coordinate of 55, proving that the point (100, 56) is not on the line. Whether or not this is an acceptable way to "show how you work out your answer" remains to be seen! |
What do you think? Drop me a comment below!
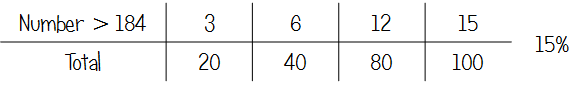
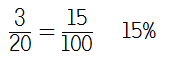
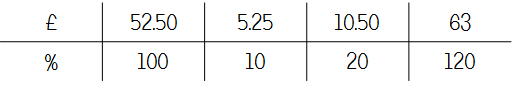
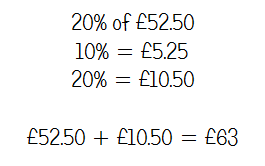
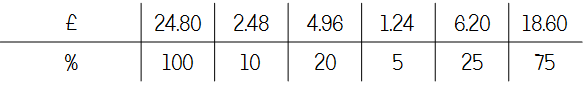
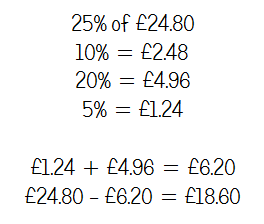
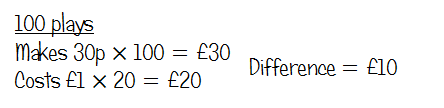
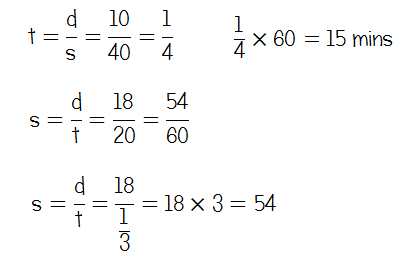
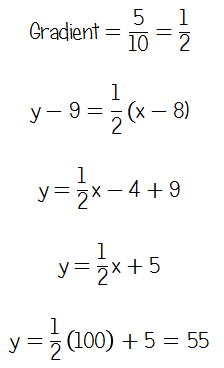
 RSS Feed
RSS Feed
