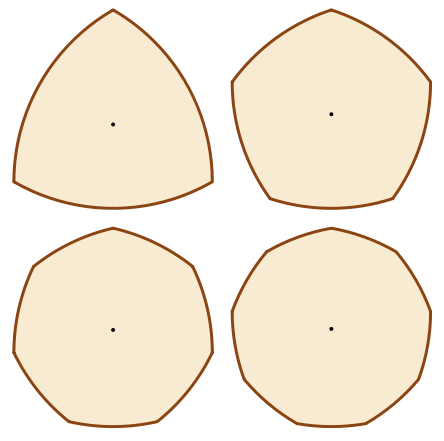
| It's going to be a quick one today as it's Friday and I'm shattered! I've just got in from work and I'm desperately trying to get this out of the way before my OH finishes work and starts demanding my attention. I'm taking my inspiration from a comment from @marcusbelben on my post about spherical and hyperbolic space - he mentioned discovering Reuleaux triangles, and this reminded me of a nice bit of maths to do with curves of constant width. Curves of constant width are pretty much as named - the width of the shape will be exactly the same wherever you measure it. A circle's the simplest example - we call its width the diameter. However, there are a whole host of other similar curves of constant width. |
You'll also recognise the heptagon-shape, as this is used for our 20p and 50p coins. Curves of constant width are great for making coins - as they have a constant diameter, their orientation doesn't matter so they'll work fine in automated coin-counting machines. They're also more difficult to forge, apparently. A few other countries have constant-curved money too - the Bermudan dollar coin is a Reuleaux triangle.
Despite all this mathematical awesomeness, we're breaking the mould in 2017 when the new12-sided £1 coins come into circulation. Apparently machines will be fine after a software upgrade, but devices such as supermarket trolleys and lockers might struggle to cope with the new coin, which won't be a curve of constant width.
If you've found this interesting, there's a segment on QI Series H: Hodge Podge that demonstrates a Reuleaux drill. Alan Davies is also given a chance to play with some 3D versions.
Image credits:
German Museum of Technology Berlin by Sterilgutassistentin - Own work, GPL,commons.wikimedia.org/w/index....
Reuleaux polygons by LEMeZza - Own work, CC BY-SA 3.0,commons.wikimedia.org/w/index....

 RSS Feed
RSS Feed
