- I taught them in Year 7, and they're a great group - very enthusiastic about maths, a bright bunch and some fantastic personalities;
- I haven't ever taught a top set at GCSE (because I teach A Level) and new experiences are always reinvigorating;
- I get to teach all of the new GCSE Higher content and explore all that;
- I'll get to do the FSMQ with them in Year 11 (yet another new experience).
However, I had a mild panic when it came to planning their first lesson this week; having chatted to their Year 9 teacher, I discovered that they know quite a lot of typical (old) Higher content already, particularly the algebra stuff. However, I wanted to make sure that they'd really got it (linking in with our Mastery curriculum) and also begin to work on their problem-solving and reasoning skills a bit more.
The mild panic was induced by the fact that I had no idea where to pitch the lesson - I'm so used to working with C/D pupils at GCSE that I had no concept of what these pupils could do and how quickly. However, the first three lessons seemed to work really well; I've really enjoyed them (and I hope the pupils have too!), so thought they should be my lesson(s) of the week.
Starting with graphs
|
After going briefly through expectations (nice not to have to do a huge spiel on this as I already know them!) and GCSE changes, we spent about thirty minutes working on a graph of two intersecting lines.
I got them to draw the graphs (thereby checking that they could actually do this quickly and accurately - a couple did need reminders!), then annotate any features they could spot. We had a class discussion about what they could see, and talked about gradients and intercepts, intersection point, why this was important, the different forms (y = mx + c and ax + by = c), constants and coefficients - I was looking to make as many links as possible and probe for prior knowledge at the same time. |
Moving to algebraic methods
|
At the end of that lesson, I asked them to show if they could find the intersection point algebraically - when I checked the books, about half of them had made a decent attempt at this using substitution. We started the next lesson with a chat about advantages and disadvantages of graphical solutions, then talked about the other two "methods" they remembered.
I wanted to get away from the idea that they'd do this type by method x and this type by method y, so we talked about how they'd see these "methods" in revision guides, but really it's just sensible use of the algebraic rules they already know. The pupils then did some practice problems - I'd picked questions that ramped up gradually and threw some fractions and negatives in. They got on with it with limited assistance, which gave me time to circulate and check they were doing things like showing their working correctly. |
The unsolvable question
|
The final question in the set of problems was this one - the pair represent the same straight line, so this was an ideal final question for getting any early finishers to really think about what was going on. Some of the very fast workers are great at applying methods quickly and accurately, but need to work on thinking carefully and analysing what's going on mathematically, and it was quite funny to watch the frustration that occured when the problem kept reducing to 16 = 16.
This led into an in-depth discussion in our third lesson about exactly what was going on in this situation; we had suggestions that the lines were parallel (as we'd discussed previously that parallel lines won't have an intersection point), then someone realised that the second rearranged to give the first. |
My lessons with this group so far have run rather like A Level lessons (aimed at a slightly lower level) - lots of discussion, taking important notes, practise and modelling my thought processes and reasoning. Whether this works well as a model for getting this group to improve their problem-solving and reasoning skills, we'll see as the weeks go on! I'm planning to start the next lesson with Matchless from Nrich to see how they tackle that.
We're going to do some more work next week on modelling and using simultaneous equations (I'd normally start with this if pupils have no prior knowledge), then probably onto a similar treatment of one linear, one quadratic with links to graphs.


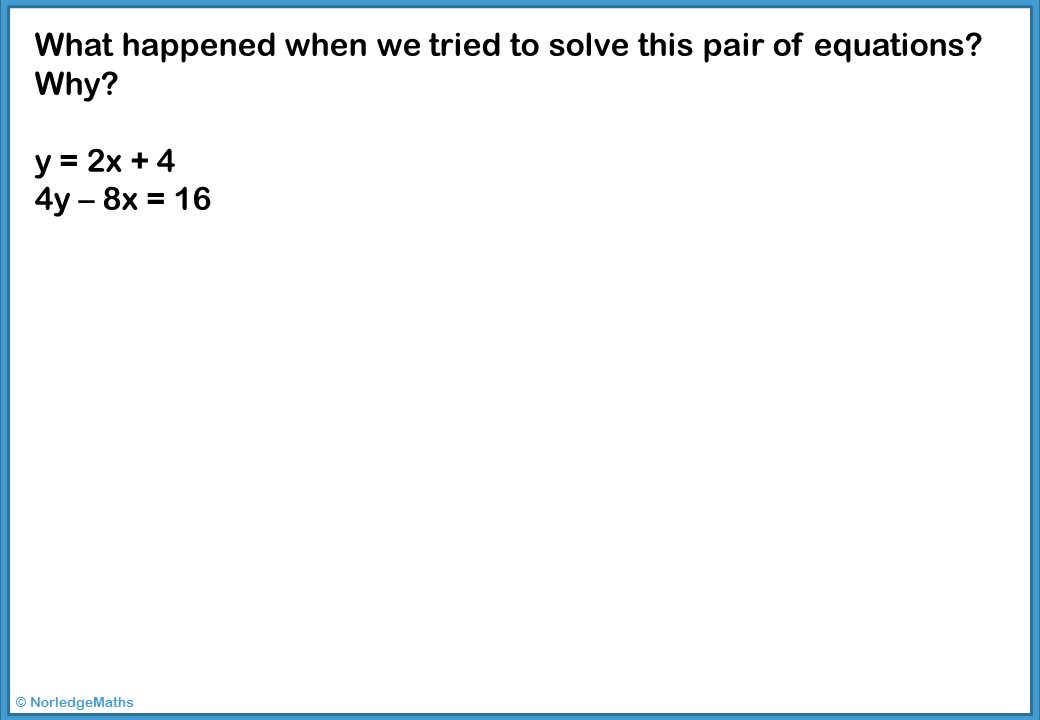
 RSS Feed
RSS Feed
