|
I'm currently a few chapters into Tony Crilly's book "How Big is Infinity"; I picked this up during a shopping trip on Easter Saturday, following an instruction from a shopping buddy that we should all "treat ourselves to something lovely" - I think she had smellies or clothes in mind; she seemed quite nonplussed that my treat was a book about maths. I'm really enjoying it so far - it's easy to dip in and out of, the chapters are quite short and it's written in real layman's terms, so it doesn't involve too many headaches or looking things up elsewhere.
|
In my third year, I decided to pick Set Theory as one of my modules, as I'd previously done Mathematical Logic and quite enjoyed the fact that Bertrand Russell (one of my favourite philosophers) kept popping up with his paradoxes. I was really interested in the ideas behind mathematics being a complete, consistent system, so Set Theory seemed like a no-brainer, and complemented one of the other modules (Computability and Countability, starring another mathematician/philosopher, Alan Turing) really well.
I remember sitting in lectures for the first few weeks not having a flipping clue what was going on. I didn't mind too much, as the lecturer had prefaced his first session by explaining that he expected most of us wouldn't understand what was going on. In fact, I eventually passed with a first equivalent on this module having only answered 50% of the exam questions, so clearly everyone else was as lost as me.
But somehow, when we got to the end of the course, it all started to make sense. I was still struggling with the (really complicated) proofs and I still couldn't draw an aleph without it looking like a complete mess, but I had the biggest lightbulb moment of my own mathematical education. I love love love the whole idea of sizes of infinity, and the weird things that come out of it - such as that there are more real numbers between 0 and 1 than natural numbers to infinity. I've done a quick run-down of the theory below if you're interested.
As a little aside, my "lightbulb moment" compares oddly to a conversation I had with a Year 11 pupil a few months ago. She'd always struggled with and hated maths, but has worked really hard despite this to get on target for a B this summer. However, in a complete about-face, she has now decided that she enjoys maths because "it's all started making sense" and she could "see the links between all of the stuff". It's interesting that this has only happened now she's finished the GCSE syllabus and is revising, and I need to reflect more on what implications this might have for my teaching.
We can distinguish between countable and uncountable infinity.
A set of numbers is countably infinite if it can be put in 1 to 1 correspondence with the natural numbers {1, 2, 3, 4, …}. An easier way to think about this is as follows.
We suppose we have an infinite amount of time (and nothing better to do!). If we can systematically list the set so that we could guarantee that each number in the set would be included at some point (i.e. it could be counted), then the set is countably infinite.
For example, the set of natural numbers is countably infinite by definition – if we began counting at 1, and counted for an infinite period of time, we could guarantee that we would have counted every single natural number.
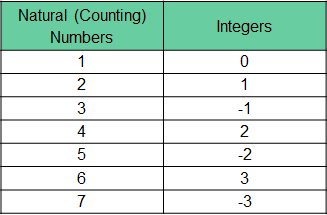
In a similar way, the set of integers is also countable. We have to be careful though – if we start at 1 and count up (1, 2, 3, 4, …), we would never reach a point when we stopped counting positive numbers and began counting negatives. Instead, we have to count in a particular way, as shown below:
It can also be shown that the primes (as a subset of the natural numbers) must be countable. The set of rational numbers is also countable (see Cantor’s diagonal proof here).
A set of numbers is uncountable if it is not countable – in other words, there’s no way to organise it in a list to ensure that each element of the set will be counted.
The set of real numbers (i.e. infinite decimal expansions) is uncountable. This is because, given any list of infinite decimals, such as 0.4524..., 0.1244..., 0.3423..., it is possible to construct a number that must differ from all of them (and therefore not be in the list), by simply defining our number as follows:
- First digit different from first number in the list;
- Second digit different from second number in the list;
- Third digit different from third number in the list... and so on.
I've used and discussed these ideas with pupils in lessons; although it's technically "degree level maths", there's an intuition behind it that makes it accessible even to Year 7.
The Open University has a lovely 60 Second Adventures in Thought video about Hilbert's Hotel, which never fails to confuse and enthuse pupils. Vi Hart's quirky Sharpie video "How many kinds of infinity are there?" is also worth a look, but is possibly too much too quickly for use in the classroom.
|
|
|

 RSS Feed
RSS Feed
