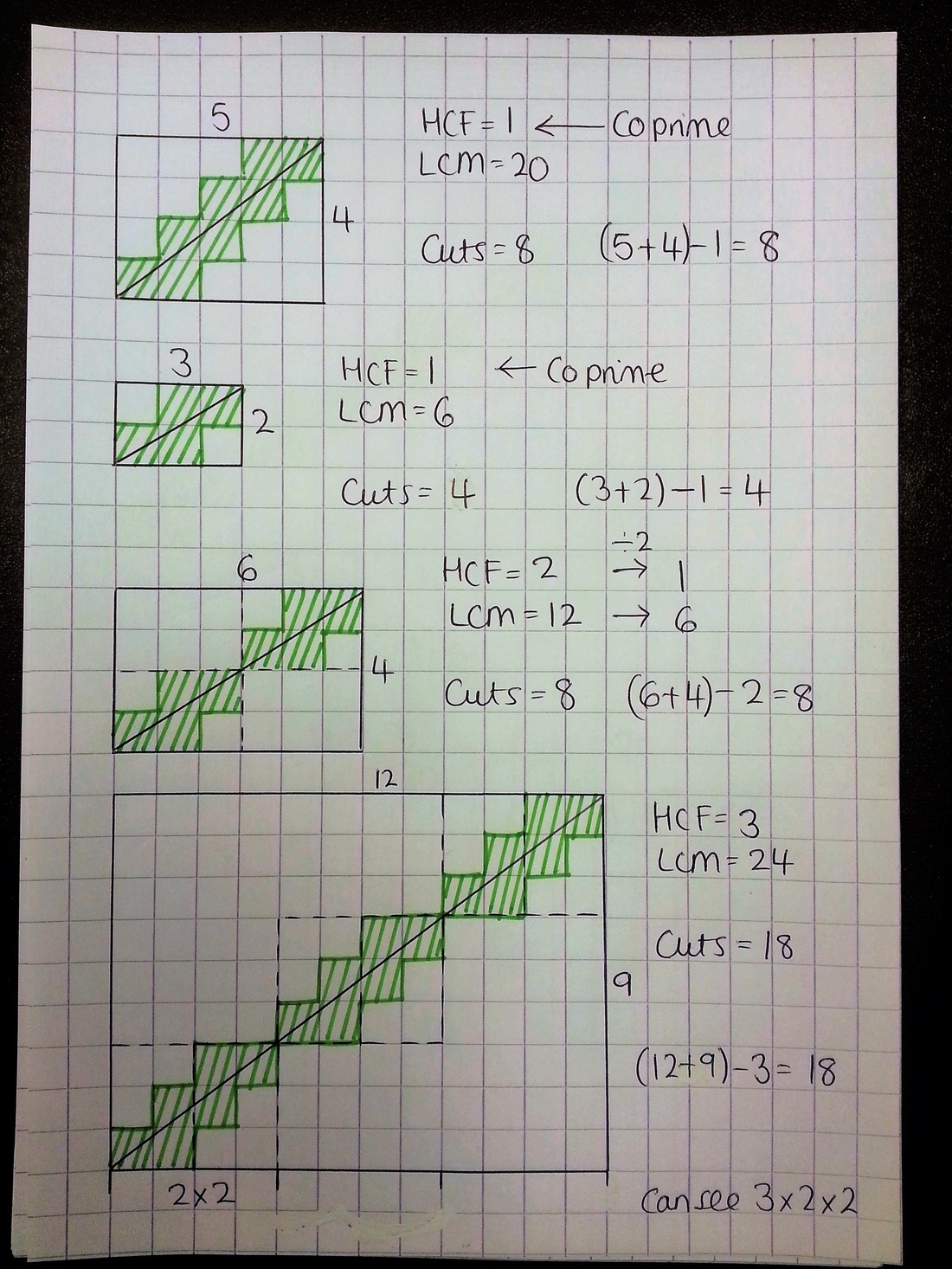
Essentially, it comes down to:
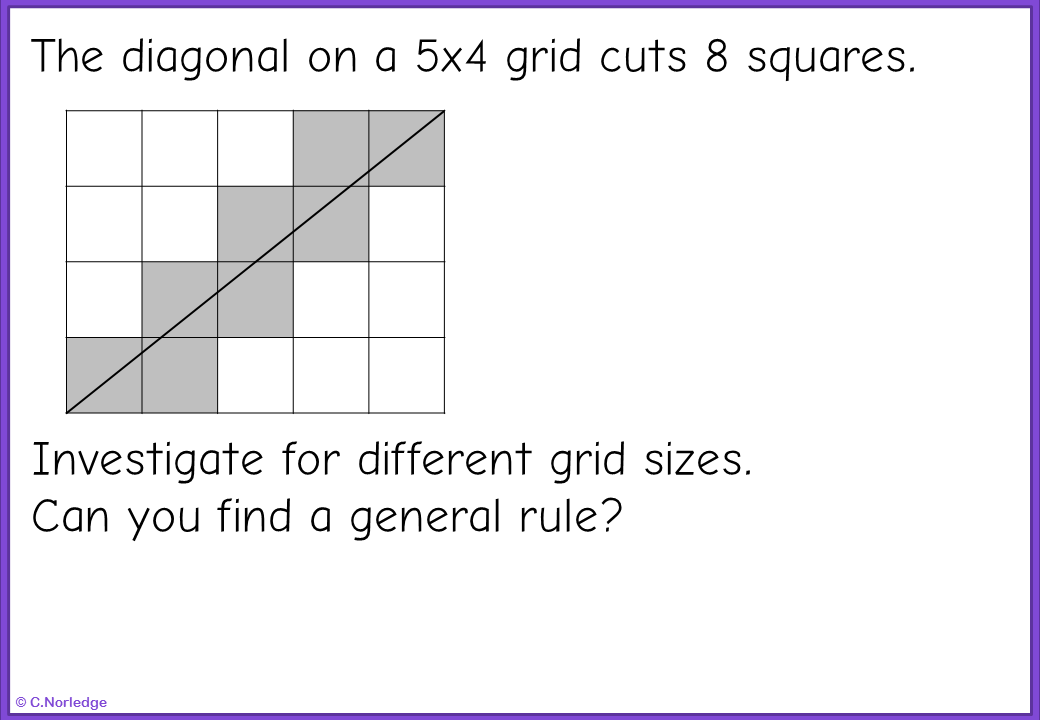
Number of cuts = (Length + Width) - HCF
It's interesting to explore the links between the 3x2 grid and the 6x4 grid. Multiplying the length and width by 2 has the effect of multiplying both the HCF and the LCM by 2. If pupils connect that grid size = HCF x LCM, there's an interesting discussion to be had here around length and area scale factors.
I also really like the connection to prime factors. It's easiest to see on a bigger grid - we can split the cut on a 12x9 into 3 lots of a 4x3 cut, creating a building block for other sizes - so you could ask pupils how many crossings in a 16x12, or 20x15, or just get them to find other grid sizes that fit with this "family".
If you examine the 4x3 block further, you can see that it's made of two 2x3 blocks, one a 180 degree rotation of the other. We can view the 2x3 as a base building block - we put two together to give the 4x3 block, then fit 3 of these along the length of the rectangle to complete a side length of 12 (see the diagram, it's much easier on there!). This gives a lovely visualisation of the product of primes for the side length of each shape.
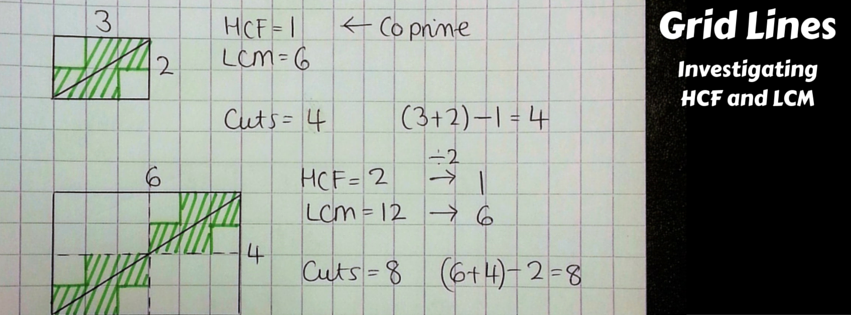
 RSS Feed
RSS Feed
