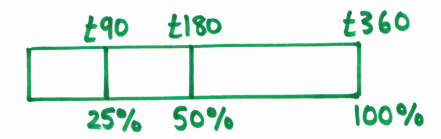
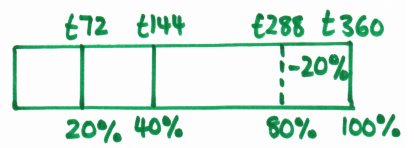
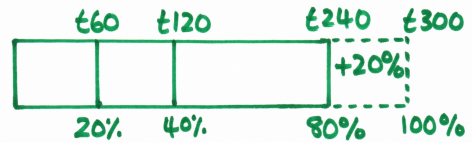
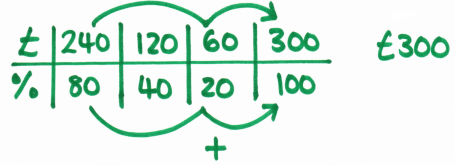
Here's the ratio table:
Ratio tables are also fantastic for other problems, such as all the proportion stuff like currency conversion. There's also a direct link to proportion graphs, as you've got your table of values to create the graph straight away.

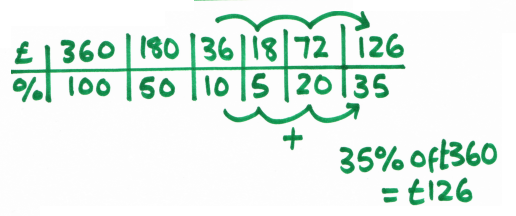


 RSS Feed
RSS Feed

Whilst these examples all provide effective ways of carrying out the calculation (without a calculator?) as soon as the problem becomes authentic the structural relationship of the reality is always one that relates to a constant of direct proportionality. That is the vertical relationship (in your bar model) is the one that matters. The horizontal number play here is helpful in carrying out the calculation not understanding the actual relationship unless it is used to find the constant of proportionality, i.e. The value of the dependent variable for one unit of the independent variable.
To help with solving real problems - that is those that arise outside of the mathematics classroom - for example in science - it is important that students understand this. How can we direct attention to this if we emphasise the bar model or ratio table so much? Would it be better to axes and graphs from the outset? Should we be emphasising ideas of variable rather than focussing on questions with only one answer? How do we cater for thinking about dependent and independent variables?
Let's widen the discussion beyond one focussed on accuracy of calculation and think about how we might ensure connections within mathematics itself and between mathematics and realities such as science and other areas of application. This would better facilitate deep understanding rather than procedural fluency.
I'd agree with most of what you've said here - I think it's really important that we teach in a way that makes pupils more aware of "the links between topics" (to talk in curriculum speak), or more accurately, that it's all just the same thing! Whenever possible (and relevant) I'd also get pupils to consider all of the points you've raised - so looking at graphical representations, finding the constants of proportionality and developing algebraic links, and also thinking about linear relationships which aren't directly proportional (and why not).
However, I don't think there needs to be an emphasis on one thing or another. It's important for pupils to have an efficient method grounded in understanding to carry out calculations, as otherwise they can't actually DO any maths with the stuff they've developed the understanding of, but it's equally important to be ensuring that pupils do experience relevant, realistic applications and work with these in depth.
With percentages "in real life", there is often one answer that we're interested in - if this item's reduced by 20%, how much will I be paying? If I have x amount in my bank account and I'm being paid 0.5% interest per year, how much will I get? I certainly wouldn't work purely with graphs for percentage calculations!
I also agree that we need to consider the examples we're using more carefully - I think there's more scope in the maths classroom to use ideas pupils will meet in the science curriculum and elsewhere, rather than make up irrelevant problems with meaningless variables.
I would say you're both (Geoff and Miss Norledge) right - it depends on the student and what they need this maths for.
Anyway, I was surprised to see these ratio tables with the £ and % rows because I thought I'd invented them during a lesson yesterday. Great minds think alike! They still didn't work for this particular student so I shall attempt manipulatives next time.
Anyway, thanks for a great page and lots of useful ideas.