This lesson began as a starter activity to work with square numbers; I was after some history of maths enrichment stuff, and decided that Fermat's Last Theorem was a great way of getting pupils to practise working with them. This starter quickly snowballed into an entire lesson, and I've used it loads since then. I decided to write about it today because it also links really nicely into one of the things I've been thinking and blogging about, namely sizes of infinity.
1. The really simple case, a + b = c
|
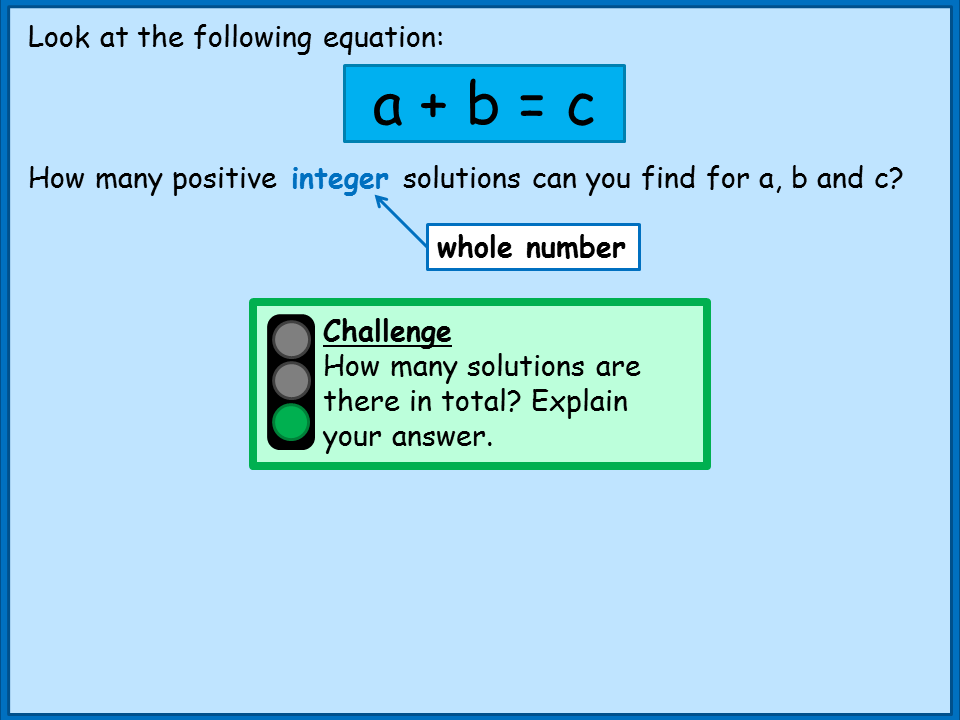
Start with a + b = c. There's lots of discussion opportunity here for probing questions:
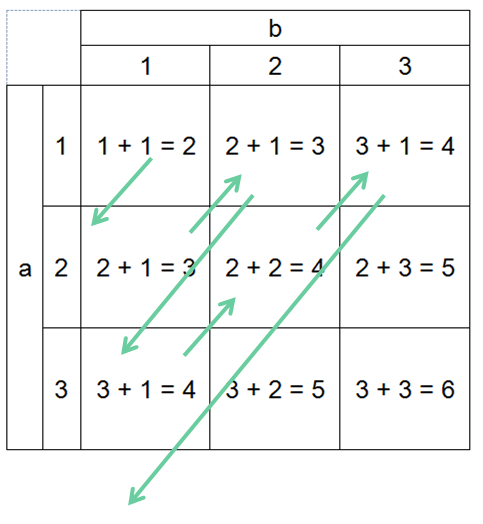
Getting pupils to work methodically (listing) is also crucial in them coming up with their answer. There's then usually a debate about infinity as a concept, not a number, with some pupils wanting to say that the number of solutions is "infinity" rather than "infinite". |
|
2. Pythagoras' theorem
|
Oh hello Pythagoras, I see you're popping up again! He worms his way into so much of mathematics.
Pupils find it much more difficult to get started with this, and writing out a list of square numbers is very useful. Once they've found one (usually 3, 4, 5), they find more very quickly by multiplying by 2, 3 etc. Sometimes I hint that there are others to look at - "there's one involving 13". Then we talk about the size of this set. Loads of them want to say that it's smaller than the previous one, because it's a subset of a + b = c, but they usually agree that it is also infinite. |
|
3. So cubes should be easy too, right?
|
Sometimes, I go straight to Fermat's Last Theorem from here and laugh as they struggle to find any solutions. The strangest thing about this is somehow the jump from squares to cubes means we go from an infinite number of solutions to no solutions at all, and it's interesting to watch pupils grapple with this idea.
Some pupils have outright refused to believe that there are no solutions, and have left the lesson swearing that they will find one and prove Fermat (and Andrew Wiles) wrong. However, branching off into a discussion about sizes of infinity is also really nice to do if time allows. |
|
4. Sizes of infinity in Fermat's Last Theorem
After a little chat about sizes of infinity (see ideas here), I sometimes go on to demonstrate how we could systematically list (and therefore count) solutions to a + b = c.
Claim: The solution set of a + b = c (a, b and c are natural numbers) is countable. |
|
A proof that a² + b² = c² is countable can be constructed similarly. It is worth noting that, as it is a subset of a + b = c, it must be countable. The solution set for a³ + b³ = c³ is trivially countable, as it is empty.
5. A bit of history
|
I finish off the lesson with a quick history lesson about Fermat and his most famous theorem, including the story about his "proof".
It is impossible to separate a cube into two cubes, or a fourth power into two fourth powers, or in general, any power higher than the second, into two like powers. I have discovered a truly marvellous proof of this, which this margin is too narrow to contain.
Fermat wrote this in a copy of Diophantus's book Arithmetica, which was one of the go-to maths textbooks of the 1600s. His son later published a version of this with all of Fermat's margin notes.
Mathematicians worked on a proof of Fermat's Last Theorem for decades. Andrew Wiles eventually proved it in 1995, and discovered/invented (depending on your view of mathematics) a load of other useful things along the way. |
|
RSS Feed
