This was the first lesson I taught using algebra tiles (you can find out about them here) and it's my go-to way to introduce completing the square now. It's worth starting with a little work on factorising first, just so you don't completely blow their minds.
|
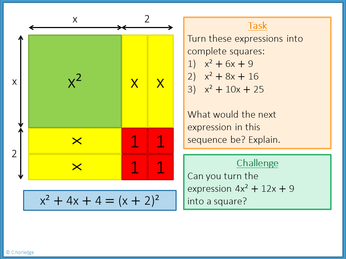
I start the lesson by considering representations of perfect squares, such as the example x² + 4x + 4, getting pupils to try to arrange the algebra tile representation of x² + 4x + 4 into a square, and pushing them towards the factored form (x + 2)². There are some lovely points for discussion of patterns in the coefficient of x and constant terms, which may be useful to draw out for further development into the “official formula” in later lessons.
Next, I get pupils to arrange x² + 4x + 3 into the best approximation to a square they can manage. They find out that they are missing one red tile to “complete” the square. We discuss the idea of being one tile short and having to “borrow” a tile to finish the square off, giving rise to (x + 2)² - 1. |
|
We then look at rearranging x² + 2x + 4 in a similar fashion, leading to the discovery that they have more tiles than they need to complete a square, and thus that x² + 2x + 4 can be written as (x + 1)² + 3, with +3 representing three additional tiles.
I then get pupils to do some on their own, using tiles and a template worksheet to support. A good challenge is to ask them to work with odd coefficients of x – pupils may suggest they need to “cut” the x strips in half, again leading nicely into development of the official formula.
I then get pupils to do some on their own, using tiles and a template worksheet to support. A good challenge is to ask them to work with odd coefficients of x – pupils may suggest they need to “cut” the x strips in half, again leading nicely into development of the official formula.
RSS Feed
